एक प्रिज्म के लिए विचलन कोण δ एवं आपतन कोण i के मध्य परिवर्तन का ग्राफ खींचिये। यदि प्रिज्म कोण A हो तो
μ=sin(A+δm2)sinA/2 संबंध का निगमन कीजिये।
एक प्रिज्म के लिए विचलन कोण δ एवं आपतन कोण i के मध्य परिवर्तन का ग्राम एवं संबंध

माना कि चित्र में ABC काँच के एक प्रिज्म का मुख्य परिच्छेद है| कोण BAC = A प्रिज्म का अपवर्तन कोण है| माना कि वायु से प्रकाश की एक किरण PQ प्रिज्म ABC के पृष्ठ AB के बिंदु Q पर अभिलंब NQE तथा पृष्ठ AC के बिंदु पर R अभिलम्ब NQE तथा पृष्ठ AC के बिंदु पर R अभिलम्ब MRE है| आपतित किरण PQ पृष्ठ AB पर अभिलम्ब NQE की ओर झुकती हुई QR दिशा में अपवर्तित होती है तथा अपवर्तित किरण QR तल AC पर अभिलम्ब MRE से दूर हटती हुई दिशा में निर्गत किरण के रूप में बाहर निकलती है| इस प्रकार चित्रानुसार, तल AB पर आपतन कोण है| AC तल पर आपतन कोण तथा निर्गत कोण है| अतः प्रिज्म में प्रकाश किरण का मार्ग PQRS है| यदि आपर्तित किरण PQ को आगे तथा निर्गत किरण RS को पीछे बढ़ाये तो वे बिंदु D पर मिलती हैं
इस प्रकार आपतित किरण संचरण दिशा से TDR कोण विचलन हो जाती है | इस कोण को विचलन कोण कहते है | अतः आपर्तित किरण तथा निर्गत किरण के बीच का कोण विचलन कोण कहलाता है ये प्रिज्म पार करने के बाद आपतित किरण जितने कोण से विचलित होती है , उसे विचलन कोण कहते है | इसे δ से प्रदर्शित करते है |
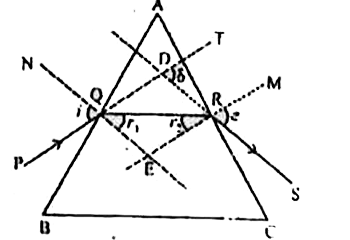
चित्र में PQRS प्रिज्म ABC में से गुजरती हुई एक प्रकाश कि किरण है | NQE तथा MRE क्रमशः प्रिज्म के AB तथा AC सतह पर अभिलम्ब है | बिंदु Q पर आपतन कोण I तथा अपवर्तन कोण r1 है बिन्दु R पर आपतन कोण r2 तथा निर्गत कोण e है | माना कि प्रिज्म का कोण ∠BAC=A है |
चतुर्भुज AQER में चारो कोणों का योग
∠A+∠AQE+∠QER+∠ERA=360∘
लेकिन ∠AQE+∠ARE=180∘
(क्योंकि प्रत्येक कोण90∘ है )
∴∠A+∠QER=180∘ ....(1)
लेकिन त्रिभुज QER में ,
∠r1+∠r2+∠QER=180∘ .....(2)
अतः समीकरण(1) व (2) से
∠A+∠r1+∠r2 ....(3)
अब त्रिभुज QDR में
δ=∠DQR+∠DRQ
(∠DQE−∠EQR)+(∠DRE−∠QRE)
या δ=(∠(i)−∠r1)+(∠e−∠r2)=(∠i+∠e)−(∠r1+∠r2) …(4)
लेकिन समीकरण (3) से
∠r1+∠r2=∠A
∴∠δ=∠i+∠e−∠A ….(3)
यदि प्रिज्म न्यूनतम विचलन कि स्थिति में हो तो δ−δm,∠i=∠e=∠i (माना )
तथा ∠r1=∠r2=∠r (माना)
समीकरण (3) से
A = 2r या r=A2 ....(6)
तथा समीकरण (5) से
δm=2i−A
या 2i=A+δm
या i=A+δm2 ....(7)
यदि μ प्रिज्म के पदार्थ का अपवर्तनांक है तो स्नैल के निम्नानुसार
μ=sinisinr
i तथा r का मान समीकरण तथा से उपर्युक्त समीकरण (6) में (7) रखने पर
μ=sin.(A+δm2)sin.A2 ....(8)
समीकरण (8) प्रिज्म सूत्र कहलाता है | इस सूत्र में यदि प्रिज्म का कोण(A) तथा न्यूनतम विचलन (δm) का मान ज्ञात हो तो प्रिज्म के पदार्थ का अपवर्तनांक ज्ञात किया जा सकता है |
Topper's Solved these Questions
Similar Questions
एक छोटी दूरबीन के अभिदृश्यक तथा नेत्रिका की फोकस दूरियाँ क्रमशः 192 cm तथा 8cm है। इसकी आवर्धन क्षमता तथा दोनों लैंसों के बीच की दूरी ज्ञात कीजिए।
View Solutionपार्श्विक विस्थापन किसे कहते हैं ? किसी दर्पण की फोकस दूरी तथा वक्रता त्रिज्या में सम्बन्ध स्थापित कीजिए।
अथवा
अवतल दर्पण के लिये किरण चित्र बनाकर सिद्ध कीजिए कि दर्पण की फोकस दूरी उसकी वक्रता त्रिज्या की आधी होती है।
View Solutionउस भौतिक राशि का नाम लिखिए जिसका मात्रक जूल/कूलॉम है। बताइये कि यह राशि सदिश है या अदिश।
View Solutionयदि प्रिज्म का कोण बहुत छोटा हों, तो सिध्द कीजिये δ=(μ−1)A,यहाँdeltaविचलनकोण,Aप्रिज्मकाकोणतथाmu प्रिज्म के पदार्थ का अपवर्तनांक है।
View Solutionसदिश 2ˆi−ˆj तथा ˆi+2ˆj के मध्य का कोण ज्ञात कीजिये।
View Solutionयदि sinθ=12 तथा θ एक अधिक कोण है , तो cotθ का मान होगा
View Solutionप्रिज्म तथा प्रिज्म द्वारा प्रकाश का अपवर्तन|प्रिज्म के पदार्थ का अपवर्तनांक तथा विचलन#!#महत्वपूर्ण प्रश्न
View Solutionदो रेखाओ के मध्य कोण
View Solutionदो समतलो के मध्य कोण
View Solutionदो समतलीय का सह-तलीय होना|दो समतलों के बीच कोण#!#समतल से दिए गए बिंदु की दूरी#!#एक रेखा एवं एक समतल के बीच कोण#!#उदाहरण
View Solutionदो रेखाओ के मध्य कोण
View Solutionदो रेखाओं के मध्य कोण
View Solutionदो समतलों के मध्य कोण
View Solutionयदि दो समतल दर्पण 90^(@) के कोण पर रखे हो तो उनके मध्य कितने प्रतिबिम्ब बनेंगे
View Solutionप्रिज्म परिचय प्रिज्म में विचलन छोटा कोण प्रिज्म
View Solutionन्यून कोण का कोण द्विभाजक | अधिक कोण का कोण द्विभाजक
View Solution
