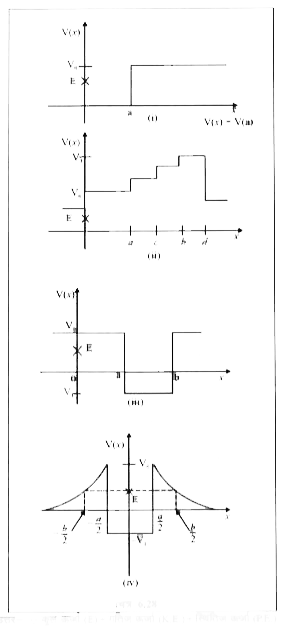
चित्र में कुछ एकविमीय स्थितिज ऊर्जा- फलनों के उदाहरण दिए गए है। कण की कुल ऊर्जा कोटि- अक्ष पर क्रॉस द्वारा निर्देशित की गई है। प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइये ,यदि कोई कार्य,ऊर्जा एवं शक्ति है तो,जिसमे दी गई ऊर्जा के लिए,कण को नहीं पाया जा सकता। इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए । कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए वे स्थितिज ऊर्जा आकृतियां प्रासंगिक हो।
कुल ऊर्जा (E) = गतिज ऊर्जा (K.E) + स्थितिज ऊर्जा (P.E)
⇒K.E=E−P.E.
∴ K.E. कभी भी ऋणात्मक नहीं हो सकती , अतः P.E.का मान सदैव E से कम ही होगा |
(i) चित्रानुसार x = 0 से x = 0 तक P.E शून्य है जिससे K.E धनात्मक है|
x>a क्षेत्र में P.E का मान E से अधिक है हो कि संभव नहीं है। अतः x>a क्षेत्र में कण उपस्थित नहीं हो सकता है।
(ii) यहाँ P.E. का मान E से अधिक है अतः वस्तु की गतिज ऊर्जा ऋणात्मक होगी जिससे कण ग्राफ के किसी भी क्षेत्र में अस्तित्व नहीं रह सकता है।
(iii) यहाँ x = 0 से x = a तथा x>b के लिए P.E का मान E से अधिक है अतः K.E का मान ऋणात्मक होगा जिससे कण इन क्षेत्रो में नहीं रह सकता है।
a<x<b में कण पाया जा सकता है तथा कण की कुल ऊर्जा −V1 है|
क्षेत्र x=−b2 से −a2 तथा x=a2 से b2 के मध्य P.E. का मान E से अधिक होने के कारण K.E. ऋणात्मक होगी। जिससे कण इस क्षेत्र में नहीं रह सकता है। तथा क्षेत्रो में कण उपस्थित रह सकता है
x<−b2,−a2<x<a2 तथा x>b2 इस स्थिति में कण की न्यूनतम कुल ऊर्जा −V1 है
Topper's Solved these Questions
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - NCERT (Text book problems) अतिरिक्त अभ्यास
7 Videos
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (लघुत्तरात्मक प्रश्न)
9 Videos
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - बोधात्मक प्रश्न
15 Videos
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न )
33 Videos
- गति के नियम BOOK - SCIENCE PUBLICATIONCHAPTER - गति के नियम EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न )
38 Videos
Similar Questions
0 . 0 12 kg द्रव्यमान की लोई गोली 70ms−1 की क्षैतिज चाल से चलते हुए 0 . 4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है। गुटके को छत से पतली तारो द्वारा लटकाया गया है। परिकलन कीजिए कि गुरका किस ऊँचाई तक ऊपर उठाया है ? गुटके में पैदा हुई उष्मा की मात्रा का भी अनुमान लगाइए।
View Solutionएक मनुष्य नदी के बहाव के विरुद्ध नाव इस प्रकार चला रहा है कि किनारे के आपेक्ष नाव स्थित रहती है। क्या मनुष्य द्वारा लगाये गये बल के द्वारा कोई कार्य किया जा रहा है ?
View Solutionसंरक्षी बलों के कुछ उदाहरण दीजिए।
View Solutionदो कण जिनके द्रव्यमान क्रमशः 100 ग्राम व 400 ग्राम है इनके स्थिति सदिश क्रमशः (2ˆi+4ˆj+2ˆk)सेमी. तथा (−6ˆi+3ˆj+2ˆk)सेमी. है। इनके द्रव्यमान केन्द्र का स्थिति सदिश ज्ञात कीजिए।
View Solution0.2 किग्रा. द्रव्यमान की क्रिकेट गेंद 20 मी./से. के वेग से गतिमान है। जिसे 0.4 सेकण्ड में विरामावस्था में लाया जाता है औसत बल की गणना कीजिए।
View Solutionसमविभव पृष्ठ | आवेशों के निकाय की स्थितिज ऊर्जा | एकल आवेश की स्थितिज ऊर्जा
View Solutionपरिवर्ती बल के लिए कार्य-ऊर्जा प्रमेय | कुछ प्रश्न
View Solutionस्थिरवैद्युत स्थितिज ऊर्जा, || बाह्य क्षेत्र में द्विध्रुव की स्थितिज ऊर्जा
View Solutionऊर्जा के विभिन्न रूप | यांत्रिक ऊर्जा |गतिज ऊर्जा तथा स्थितिज ऊर्जा | संवेग और गतिज ऊर्जा में सम्बन्ध |किसी स्प्रिंग की स्थितिज ऊर्जा
View Solutionकार्य ऊर्जा प्रमेय ॥परिवर्ती बल के लिए कार्य-ऊर्जा प्रमेय | यांत्रिक ऊर्जा का संरक्षण | कुछ प्रश्न
View Solutionसजीवों को ऊर्जा के लिए .....तथा श्वसन की आवश्यकता होती है।
View Solutionतरलों के यांत्रिकी गुण |प्रवाहित तरल की ऊर्जा #!#गतिज ऊर्जा #!#स्थितिज ऊर्जा#!#दाब ऊर्जा
View Solutionमीथेन और अथेन के समान दृव्यमानो की कुल स्थानांतरण गतिज ऊर्जा 3:1 के अनुपात में है तो उनके तापमानों में अनुपात होगा
View SolutionH-परमाणु की प्रथम कक्षा में एक इलेक्ट्रॉन की ऊर्जा −13.6eV है। Li2+ आयनों की बोर कक्षाओं में इलेक्ट्रॉनों के लिए उत्तेजित अवस्था में संभावित ऊर्जा मान है/हैं-
View Solutionहाइड्रोजन के समान एक काल्पनिक परमाणु के लिए, निकाय की स्थितिज ऊर्जा U (1) = (-ke^2)/(r^3) द्वारा दी जाती है, जहाँ r दो कणों के बीच की दूरी है। यदि कोणीय संवेग के क्वान्टीकरण का बोर मॉडल लागू होता है, तो कण का वेग निम्नलिखत में किसके द्वारा दिया जाता है?
View Solutionनिम्नलिखित में से किसके लिए ऊर्जा की मात्रा अधिकतम है?
View Solution
