कॉलम - I में मानक यंग की द्विस्लिट व्यवस्था की चार स्थितियाँ दिखाई गई हैं जिसमें परदा, S1 और S2 स्लिटों से काफ़ी दूर रखा जाता है। इन सब में S1P0=S2P0,S1P1−S2P1=λ/4 और S1P2−S2P2=λ/3 । स्थितियों B , C और D में μ अपवर्तनांक और t मोटाई की पारदर्शी शीट , स्लिट S2 पर चिपका दी जाती है। अलग - अलग स्थितियों में शीटों की मोटाइयाँ अलग - अलग हैं। दोनों स्लिटों से परदे पर P बिन्दु पर पहुँच रही प्रकाश तरंगों के बीच कलान्तर , δ(P) से निर्दिष्ट किया जाता है और तीव्रता , I (P) से। कॉलम - I में दी गई हर स्थिति को उस स्थिति के लिए वैध
कॉलम - II के कथन से मिलाएँ
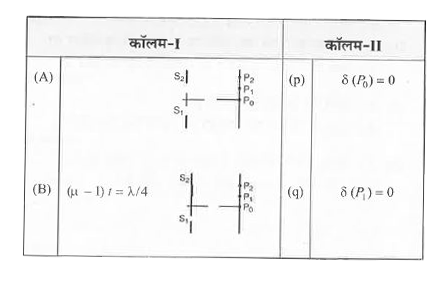
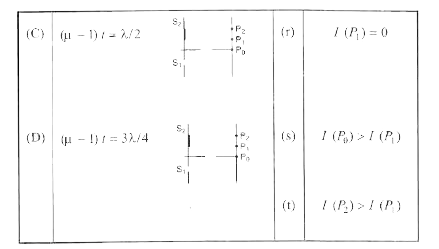
(A→p,s),(B→q),(C→t),(D→r,s,t)
Topper's Solved these Questions
- तरंग प्रकाशिकीBOOK - GRB PUBLICATION HINDICHAPTER - तरंग प्रकाशिकीEXERCISE - प्रतियोगिता सामग्री कथन-कारण -आधारित प्रश्न
31 Videos
- तरंग प्रकाशिकीBOOK - GRB PUBLICATION HINDICHAPTER - तरंग प्रकाशिकीEXERCISE - प्रतियोगिता सामग्री पूर्णक उत्तर वाले प्रश्न
11 Videos
- तरंग प्रकाशिकीBOOK - GRB PUBLICATION HINDICHAPTER - तरंग प्रकाशिकीEXERCISE - प्रतियोगिता सामग्री बहुविकल्पीय प्रश्न : एक सही विकल्प
169 Videos
- चुम्बकत्वBOOK - GRB PUBLICATION HINDICHAPTER - चुम्बकत्वEXERCISE - प्रतियोगिता सामग्री रिक्त स्थान भरना
12 Videos
- द्रव्य तथा विकिरण की द्वैत प्रकृति BOOK - GRB PUBLICATION HINDICHAPTER - द्रव्य तथा विकिरण की द्वैत प्रकृति EXERCISE - प्रतियोगिता सामग्री (रिक्त स्थान भरना)
14 Videos
Similar Questions
A : निर्वात में अलग-अलग रंग, अलग-अलग चालो से चलते है।
R : प्रकाश का तरंगदैर्ध्य, माध्यम के अपवर्तनांक पर निर्भर है।
View Solution3cm ऊँची वस्तु, 40cm वक्रता व्यासार्ध वाले एक अवतल दर्पण से 50cm की दूरी पर है। प्रतिबिम्ब का आकर…. है।
View Solution(12(i+√3j)) दिशा में चल रही प्रकाश की एक किरण , एक समतल दर्पण पर आपतित होती है। परावर्तन के बाद यह (12(i−√3j)) दिशा में जाती है। आपतन कोण है
View Solutionएक छड़ चुम्बक को इसकी लम्बाई के लम्बवत दो बराबर टुकड़ों में काटने से एक ही ध्रुव तीव्रता परन्तु.........द्विध्रुव आघूर्ण वाले चुम्बक उत्पन्न होते हैं।
View Solutionप्रकाश - वैद्युत प्रभाव……. से होता है।
View SolutionLet Sn=1+2+3++n and Pn=S2S2−1⋅S3S3−1⋅S4S4−1⋅⋅⋅SnSn−1 Where n∈N,(n≥2). Then limx→∞Pn=______
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
The coordinates of P1 are
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
The ratio area(ΔP1P2P3)area(ΔC1C2C3) is equal to
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
P2 and P3 are images of each other with respect to the line
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. The co-ordinates of P1 are :
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. The ratio area(ΔP1P2P3)area(ΔC1C2C3) is equal to :
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. P2andP3 are image of each other with respect to line :
View Solutionα,β,γ are the roots of the cubic equation x3+p1x2+p2x+p3=0. If Sr=αr+βr+γr,S1=10,S2=38 and S3=−1840, then p3=
View Solutionα,β,γ are the roots of the cubic equation x3+p1x2+p2x+p3=0. If Sr=αr+βr+γr,S1=10,S2=38 and S3=−1840, then p3=
View Solutionस्तम्भ I में स्टैण्डर्ड यंग द्वि - स्लिट विन्यास की चार परिस्थितयाँ दिखाई गई है | जिनमें स्लिट S1 तथा S2 स्क्रीन से काफी दूरी पर है | प्रत्येक परिस्थिति में S1P0=S2P0,S1P1−S2P1=λ/4 और S1P2−S2P2=λ/3, जहाँ λ प्रकाश की तरंगदैर्ध्य है | B, C व D परिस्थितियों में स्लिट S1 के सामने μ अपवर्तनांक और t मोटाई की पारदर्शी शीट रखी गई है | इन सीटों की मोटाई प्रत्येक परिस्थिति में भिन्न - भिन्न है | स्क्रीन के किसी बिंदु P पर दोनों स्लिट से पहुँच रही प्रकाश तरंगों के फेज - अंतर को S( P ) से निरूपित किया गया है | तथा प्रकाश की तीव्रता को I ( P ) से निरूपित किया गया है | स्तम्भ I की प्रत्येक परिस्थितियों के लिए स्तम्भ II के प्रकथनों को आपस में मिलाइए |
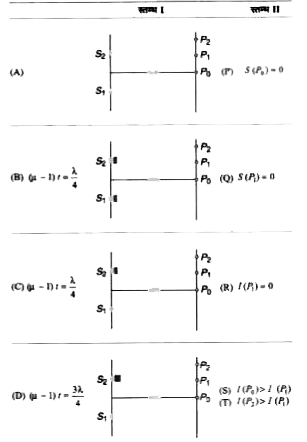
View Solution
