वृत्त के केन्द्र के परितः सममित रूप से, वृत्त के व्यास पर, x दूरी पर दो समान कला-सम्बद्ध स्रोत स्थित हैं। वृत्त की त्रिज्या R(x<<R) है। वृत्त पर स्थित बिन्दु-स्रोतों की अधिकतम तीव्रता (x=5λ) है
20
22
24
26
The correct Answer is:A
आरेख द्वारा,
पथान्तर =S1M=P
P=S1M=xcosθ (∵x<<R)
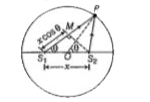
(माना कि S1PऔरS2P लगभग समान्तर है) अधिकतम तीव्रता के लिए, P=nλ
(जहाँ, n = 0,1,2,3)
⇒xcosθ=nλ
⇒cosθ=nλx
⇒cosθ=nλ5λ (x=5λ)
⇒cosθ=n5
हम जानते हैं, −1,≤cosθ≤1
⇒−1≤n5≤1⇒−5≤n≤5
n के सम्भावित मान
={0,±1,±2,±3,±4,±5}
माना कि प्रत्येक मान के लिए θ परास में हैं।
θ≠(0,2π)
n=1के लिएcosθ=15
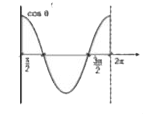
यहाँ, n के ऋणात्मक मान का अर्थ है कि पथान्तर (S1P−S2P) भी ऋणात्मक होगा। इन बिन्दुओं के लिए, S1P<S2P
n=0,±1,±2,±3,±4 के लिए, कोज्या फलन के दिए गए आरेख में अन्तराल θ∈[0,2π] n के ऊपर दिए गए मानों के लिए कुल 18 बिन्दु हैं अर्थात् 2 बिन्दु n=0 के लिए, 4 बिन्दु n=±1,±2,±3,±4 में प्रत्येक के लिए
n= + 5 के लिए, cosθ=+1
θ का एक मान है अर्थात् θ=2π के लिए θ=0∘ सम्भव है। ये बिन्दु सम्पाती होगें।
=-5 के लिए, cosθ=−1 अर्थात् θ=π
अत: 4 चतुर्थांशों में 20 उच्चिष्ठ बिन्दु सम्भव होंगे।
Similar Questions
खण्ड 'अ'खण्ड 'ब'1.वृत्त के अन्तः बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(a)समकोण2.वृत्त के किसी बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(b)स्पर्श रेखा3.वृत्त के बाह्य बिंदु से वृत्त पर खींची गयी स्पर्श रेखाओं की संख्या(c)शून्य4.स्पर्श रेखा और स्पर्श बिंदु से जाने वाली त्रिज्या के बीच बना कोण(d)एक5.वृत्त को केवल एक बिंदु पर प्रतिच्छेद करने वाली रेखा(e)दो
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View SolutionIf the length of a chord of a circle C at a distance of 12 cm from the centre is 10 cm, then the diaimeter of the circle is यदि किसी वृत्त के केन्द्र से 12 सेमी. की दूरी पर जीवा की लंबाई 10 सेमी. है, तो वृत्त का व्यास है-
View Solutionवृत्त का व्यास | वृत्त के सापेक्ष बिंदुओं की स् थिति
View SolutionIn a circle two equal and parallel chords are 6 cm apart and lie on the opposite sides of the centre of the circle.If the length of each chord is 8 cm, than the radius of the circle is: एक वृत्त में दो बराबर और समान्तर जीवाएँ 6 cm के दुरी पर हैं और वृत्त के केंद्र के विपरीत भाग पर स्थित हैं। यदि प्रत्येक जीवाएँ की लंबाई 8 सेमी है, तो वृत्त की त्रिज्या है:
View SolutionIn a circle, two equal and parallel chords are 6 cm apart and they lie on the opposite sides of the centre of the circle, whose radius is 5 cm. The length of each chord (in cm), is एक वृत्त में, दो समान और समानान्तर जीवा 6 सेमी के दुरी पर हैं और वे वृत्त के केंद्र के विपरीत किनारों पर स्थित हैं, जिसकी त्रिज्या 5 सेमी है। प्रत्येक जीवा की लंबाई (सेमी में ) है:
View SolutionTwo circles of radii 7 cm and 9 cm intersect at the points A and B. If AB=6cm, and the distance between the centres of the circles is x cm, then the value of x (to the closest integer) is: 7 cm और 9 cm त्रिज्या के दो वृत्त, बिंदु A और B पर एक दूसरे को काटते हैं| अगर AB=6 cm है, और वृत्त के केंद्रों के बीच की दूरी x cm है तो x का मान (निकटतमें पूर्णाक में) है:
View Solution
