In a circle two equal and parallel chords are 6 cm apart and lie on the opposite sides of the centre of the circle.If the length of each chord is 8 cm, than the radius of the circle is:
एक वृत्त में दो बराबर और समान्तर जीवाएँ 6 cm के दुरी पर हैं और वृत्त
के केंद्र के विपरीत भाग पर स्थित हैं। यदि प्रत्येक जीवाएँ की लंबाई 8 सेमी है, तो वृत्त की त्रिज्या है:
5 cm
7 cm
3 cm
2 cm
Step by step video & image solution for In a circle two equal and parallel chords are 6 cm apart and lie on the opposite sides of the centre of the circle.If the length of each chord is 8 cm, than the radius of the circle is: एक वृत्त में दो बराबर और समान्तर जीवाएँ 6 cm के दुरी पर हैं और वृत्त के केंद्र के विपरीत भाग पर स्थित हैं। यदि प्रत्येक जीवाएँ की लंबाई 8 सेमी है, तो वृत्त की त्रिज्या है: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
Similar Questions
In a circle, two equal and parallel chords are 6 cm apart and they lie on the opposite sides of the centre of the circle, whose radius is 5 cm. The length of each chord (in cm), is
एक वृत्त में, दो समान और समानान्तर जीवा 6 सेमी के दुरी पर हैं और वे वृत्त के केंद्र के विपरीत किनारों पर स्थित हैं, जिसकी त्रिज्या 5 सेमी है। प्रत्येक जीवा की लंबाई (सेमी में ) है:View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively, are parallel and are on the same side of the centre O of a circle. If the distance between the chords is 3 cm, then what is the diameter of the circle?
लंबाई क्रमशः 5 सेमी और 11 सेमी की दो जीवाएं AB और CD समानांतर हैं तथा वृत्त के केंद्र O के एक ही तरफ स्थित हैं | यदि जीवाओं के बीच की दूरी 3 सेमी है, तो वृत्त का व्यास क्या होगा ?View SolutionIn a circle centred at O, AB is a chord and C is any point on AB, such that OC is perpendicular to AB. If the length of the chord is 16 cm and OC = 6 cm, the radius of circle is :
O केंद्र वाले एक वृत्त में, AB एक जीवा है और C, AB पर कोई बिंदु है, जैसे OC, AB पर लंबवत है। यदि जीवा की लंबाई 16 सेमी और OC = 6 सेमी है, तो वृत्त की त्रिज्या है:View SolutionIn a circle centred at O, AB is a chord and C is any point on AB, such that OC is perpendicular to AB. If the length of the chord is 16 cm and OC = 6 cm, the radius of circle is :
O क वाले एक वृत्त में, AB एक जीवा है और C, AB पर कोई बिंदु है, जैसे OC, AB पर लंबवत है। यदि जीवा की लंबाई 16 सेमी और OC = 6 सेमी है, तो वृत्त की त्रिज्या है:View SolutionTwo circles touch each other externally. The distance between their centres is 8 cm. If the radius of one circle is 3 cm, then the radius of the other circle is:
दो वृत्त एक दूसरे को बाह्य रूप से स्पर्श करते हैं। उनके केंद्रों के बीच की दूरी 8 सेमी है। यदि एक वृत्त की त्रिज्या 3 सेमी है, तो दूसरे वृत्त की त्रिज्या है:View SolutionA circle has two parallel chords of lengths 6 cm and 8 cm. If the chords are 1 cm apart and the centre is on the same side of the chords, then a diameter of the circles is of length:
View SolutionA circle has two parallel chords of lengths 6 cm and 8 cm. If the chords are 1 cm apart and the centre is on the same side of the chords, then a diameter of the circles is of length:
View SolutionAB and CD are two parallel chords of a circle such that AB = 6 cm and CD = 2AB. Both chords are on the same side of the centre of the circle. If the distance between is equal to one-fourth of the length of CD, then the radius of the circle is-
AB और CD किसी वृत्त की दो ऐसी समानांतर जीवाएं है कि AB = 6 सेमी है और CD = 2AB है | दोनों जीवाएं वृत्त के केंद्र के एक ही तरफ हैं | यदि बीच की दूरी CD की लंबाई के एक चौथाई के बराबर है, तो वृत्त की त्रिज्या ज्ञात करें |View SolutionIn the given figure, TB is a chord which passes through the centre of the circle. PT is a tangent to the circle at the point. T on the circle. If PT = 10 cm, PA = 5 cm and AB = x cm, then the radius of the circle is:
दिए गए चित्र में, TB एक जीवा है जो वृत्त के केंद्र से होकर गुजरता है। PT, वृत्त के बिंदु T पर वृत्त की स्पर्शरेखा है। यदि PT= 10 सेमी, PA=5 सेमी और AB = x सेमी, तो वृत्त का त्रिज्या है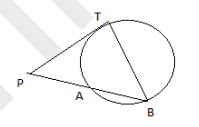 View Solution
View SolutionThe radius of a circle is 15 cm and the length of one chord of the circle is 20 cm. What is the distance of the chord from the centre of the circle?
एक वृत्त की त्रिज्या 15 सेमी है और वृत्त के एक जीवा की लंबाई 20 सेमी है। वृत्त के केंद्र से जीवा की दूरी क्या है?View Solution


