किसी पुस्तक में, जिसमे छपाई की अनेक त्रुटिया हैं, आवर्त गति कर रहे किसी कण के विस्थापन के चार भिन्न सूत्र दिय गए हैं :
(a) y=asin2πt/T
(b) y=asinvt
(c) y=(a/T)sint/a
(d) y=(a√2)(sin2πt/T+cos2πt/T)
(a = कण का अधिकतम विस्थापन, v = कण की चाल, T = गति का आवर्त काल) । विमीय आधारों पर गलत सूत्रों को निकाल दीजिए ।
(a) y=a sin2πtT विमीय आधार पर सही है, क्योंकि कोण 2πtT विमाहिन है तथा a व y दोनों कि विमा [L] है ।
(b) y=asinvt विमीय आधार पर गलत है, क्योंकि vt कि विमा [LT−1][T]=[L] है जबकि कोण vt विमाहिन होना चाहिए ।
(c) y=(aT))sinta विमीय आधार पर गलत है, क्योंकि कोण ta कि विमा [TL]=[L−1T] है जबकि कोण विमहीन होना चाहिए, इसके अतिरिक्त y कि विमा [L] तथा [aT] कि विमा [LT−1] है, जो विमीय संतुलन-सिध्दांतो के विपरीत हैं ।
(d) y=a√2(sin2πtT+cos2πtT) विमीय आधार पर सही है, क्योंकि कोण 2πtT विमाहिन है तथा y व a√2 दोनों कि विमा [L] है ।
Topper's Solved these Questions
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - अतिरिक्त प्रश्न
9 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
9 Videos
- मात्रक, मापन तथा त्रुटि विश्लेषण BOOK - NOOTAN HINDICHAPTER - मात्रक, मापन तथा त्रुटि विश्लेषण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
19 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
Similar Questions
वर्षा के समय में कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है । उसे अपने छाते को टेढ़ा करके उर्ध्व के साथ θ कोण बनाना पड़ता है । कोई विद्यार्थी कोण θ व v के बीच निम्नलिखित संबंध व्युतपन्न करता है :
tanθ=v,
और वह इस संबंध के औचित्य की सिमा पता लगाता है, जैसी की आशा की जाती है यदि v → 0 तो θ→0 | (हम यह मान रहे हैं की तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा उर्ध्वाधरत: पद रही है) । क्या आप सोचते हैं की यह संबंध सही हो सकता है ? यदि ऐसा नहीं है तो सही संबंध का अनुमान लगाइए ।
View Solutionदूरी z के साथ दाब P का विचरण, P=αβe−az/kθ से व्यक्त किया जाता है, जहाँ α,β नियतांक हैं, k बोल्ट्समान नियतांक तथा θ ताप है । β का विमीय सूत्र होगा :
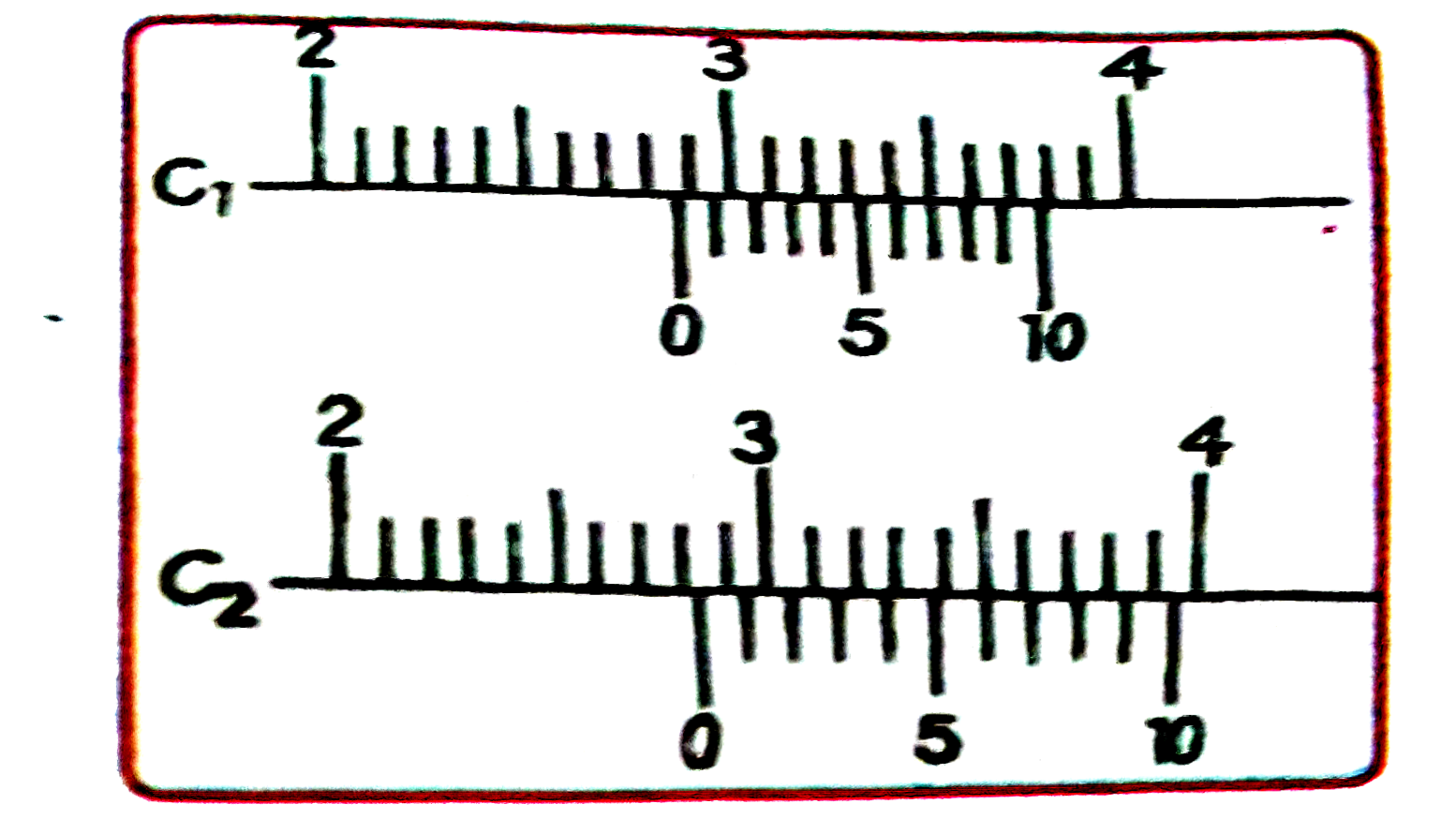
View Solutionदो वर्नियर कैलिपर्स इस तरह से हैं कि उनके मुख्य पैमाने का 1 समी, 10 समभागों में विभाजित है। एक कैलिपर (C1) के वर्नियर पमाने पर 10 बराबर भाग हैं जो कि मुख्य पैमा के 9 भागों के बराबर है। दूसरे कैलिपर (C2) के वर्नियर पैमाने पर भी 10 बराबर भाग हैं जो कि मुख्य पैमाने के 11 भागों के बराबर हैं। दोनों कैलिपर्स के पठनों को चित्र में दर्शाया गया है। C1 तथा C2 द्वारा मापे गए सही मान (सेमी में) क्रमश: हैं :
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View SolutionIf x=a(cost+tsint)and y=a (sin t - t cos t), then find the value of d2ydx2 at t=π4 .
View SolutionIf x=a(cost+tsint) and y=a(sint−tcost), then find the value of d2ydx2
View Solutionx=tcost,y=t+sint. Then d2xdy2a=π2 is π+42 (b) −π+42 −2 (d) none of these
View Solutionx=a cos t,y=a sin t then (d^(2)(y))/(dx^(2)) at t=(pi)/(3),(pi)/(6),(pi)/(2),(pi)/(4)
View SolutionIf x=a(sin t-t cos t),y=a sin t then find the value of (d^(2)y)/(dx^(2))
View SolutionIf x=a(cost+tsint) and y=a(sint−tcost) , then find the value of d2ydx2 .
View SolutionIf x=a(cost+logtan(t2)) , y=asint , evaluate d2ydx2 at t=π3 .
View Solutionx=t cos t,y=t+sin t. Then (d^(2)x)/(dy^(2)) at t=(pi)/(2) is
View SolutionIf x=sint−tcostandy=tsint+cost, then what is dydx
at point t=π2?
View SolutionIf x=sint and y=sin3t, then d2ydx2 at t=π2 is
View Solutionयदि x=a(cost+tsint),y=a(sint−tcost), तो t=π4परd2ydx2 ज्ञात कीजिए ।
View Solution
