कोई भौतिक राशि P, चार प्रेक्षण-योग्य राशियों a, b, c तथा d से इस प्रकार संबंधित है :
P=a3b2/(√cd)
a, b, c तथा d के मापने में प्रतिशत त्रुटियाँ क्रमश : 1%, 3%, 4% तथा 2% हैं । राशि P में प्रतिशत त्रुटि कितनी है ? यदि उपर्युक्त संबंध का उपयोग करके P का परिकलित मान 3.763 आता है, तो आप परिमाण का किस मान तक निकटन करेंगे ?
P=a3b2d√c=a3b2c−1/2d−1
P के मान में भिन्नात्मक त्रुटि
ΔPP=3Δaa+2Δbb−12Δcc−Δdd
P के मान में अधिकतम भिन्नात्मक त्रुटि
∣∣∣ΔPP∣∣∣max=3Δaa+2Δbb+12Δcc+Δdd
P के मान में अधिकतम प्रतिशत त्रुटि
∣∣∣ΔPP∣∣∣max×100=3(Δaa×100)+2(Δbb×100)+12(Δcc×100)+(Δdd×100)
= 3(a में प्रतिशत त्रुटि) + 2(b में प्रतिशत त्रुटि) +112 (c में प्रतिशत त्रुटि) + (d में प्रतिशत त्रुटि)
=3%(1%)+2(3%)+12(4%)+(2%)
= 3% + 6% + 2% + 2% = 13%.
गणना द्वारा प्राप्त P का मान 3.763 है । P के मान में प्रतिशत त्रुटि 13% है । अंत: P के मान में त्रुटि
ΔP=3.763×13100=0.48919≈0.5
चूँकि P के मान में त्रुटि दशमलव के प्रथम स्थान में हैं, अंत: P का मान 3.763 भी दशमलव के प्रथम स्थान तक पूर्ण किया जाना चाहिए । इस प्रकार,
P = 3.8 (उचित सार्थक अंको तक)
अंत: अंतिम परिणाम P = 3.8 ± 0.5.
Topper's Solved these Questions
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - अतिरिक्त प्रश्न
9 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
9 Videos
- मात्रक, मापन तथा त्रुटि विश्लेषण BOOK - NOOTAN HINDICHAPTER - मात्रक, मापन तथा त्रुटि विश्लेषण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
19 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
Similar Questions
वर्षा के समय में कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है । उसे अपने छाते को टेढ़ा करके उर्ध्व के साथ θ कोण बनाना पड़ता है । कोई विद्यार्थी कोण θ व v के बीच निम्नलिखित संबंध व्युतपन्न करता है :
tanθ=v,
और वह इस संबंध के औचित्य की सिमा पता लगाता है, जैसी की आशा की जाती है यदि v → 0 तो θ→0 | (हम यह मान रहे हैं की तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा उर्ध्वाधरत: पद रही है) । क्या आप सोचते हैं की यह संबंध सही हो सकता है ? यदि ऐसा नहीं है तो सही संबंध का अनुमान लगाइए ।
View Solutionदूरी z के साथ दाब P का विचरण, P=αβe−az/kθ से व्यक्त किया जाता है, जहाँ α,β नियतांक हैं, k बोल्ट्समान नियतांक तथा θ ताप है । β का विमीय सूत्र होगा :
View Solutionदो वर्नियर कैलिपर्स इस तरह से हैं कि उनके मुख्य पैमाने का 1 समी, 10 समभागों में विभाजित है। एक कैलिपर (C1) के वर्नियर पमाने पर 10 बराबर भाग हैं जो कि मुख्य पैमा के 9 भागों के बराबर है। दूसरे कैलिपर (C2) के वर्नियर पैमाने पर भी 10 बराबर भाग हैं जो कि मुख्य पैमाने के 11 भागों के बराबर हैं। दोनों कैलिपर्स के पठनों को चित्र में दर्शाया गया है। C1 तथा C2 द्वारा मापे गए सही मान (सेमी में) क्रमश: हैं :
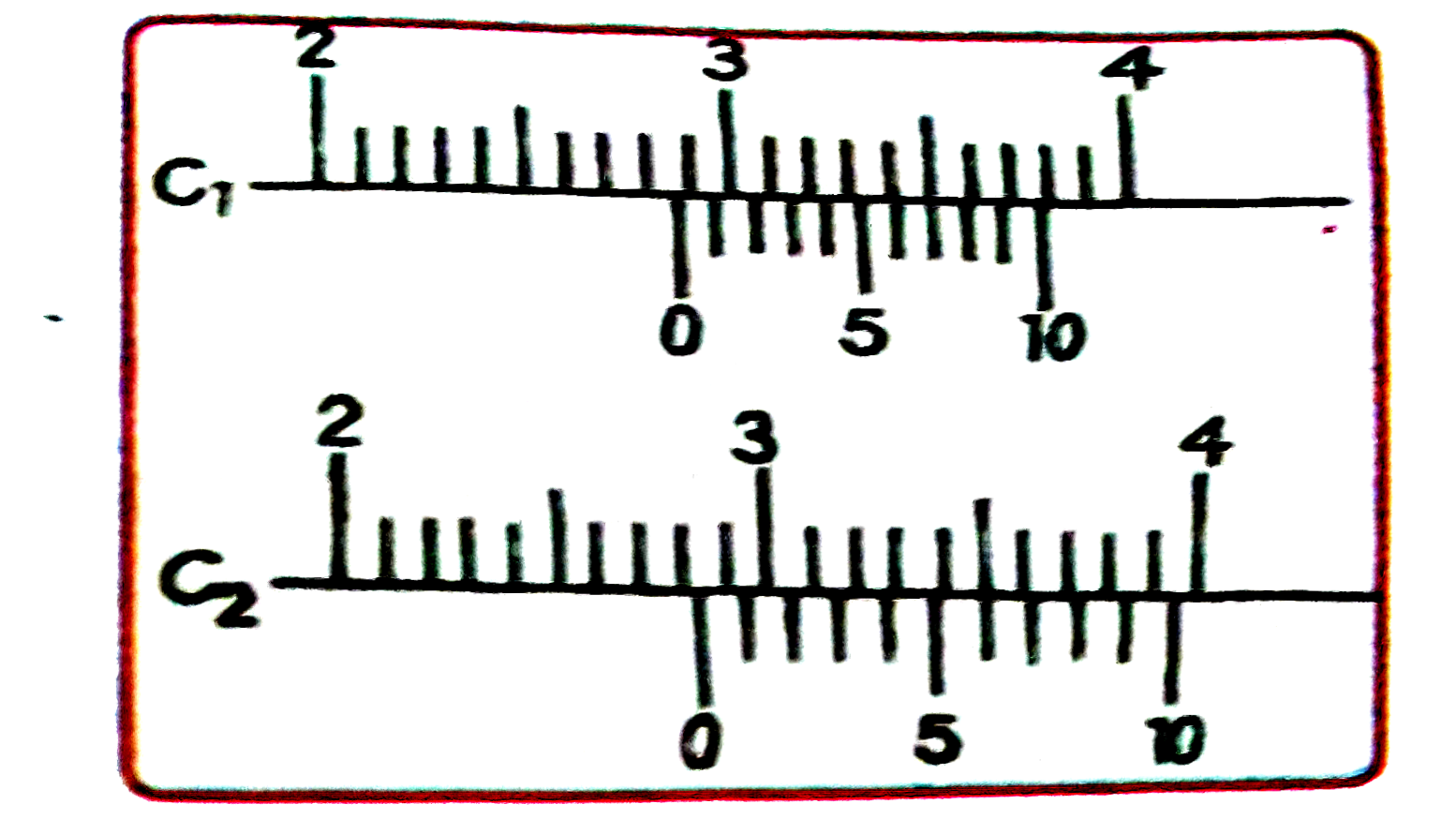
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
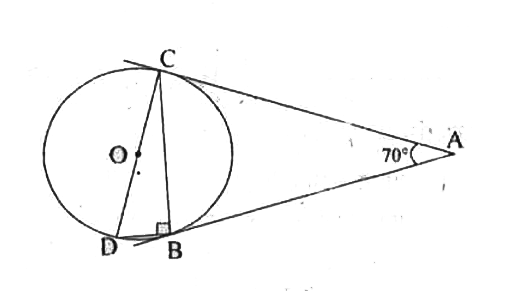
View Solutionयदि दो घटनाएँ A तथा B इस प्रकार से है कि P(A)=1/4, P(B)=1/2 तथा P(bar A nn bar B) ज्ञात कीजिये।
View Solutionएक निर्माता के पास तीन यंत्र संचालक A,BतथाC हैं। प्रथम संचालक A, 1% त्रुटिपूर्ण वस्तुएं उत्पादित करता है, जबकि अन्य दो संचालक B तथा C क्रमश: 5% तथा 7% त्रुटिपूर्ण वस्तुएं उत्तपादित करते है। A कार्य पर कुल स्म्य का 50% लगता है, B कुल स्म्य का 30% लगता है तथा C कुल स्म्य का 20% लगता है। यदि एक त्रुटिपूर्ण वस्तु उत्पादित है तो इसकी क्या प्रायिकता है कि यह यंत्र A से उत्पादित है?
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View SolutionThe average of two numbers A and B is 20, that of B and C is 19 and of C and A it is 21. What is the value of A? दो संख्याओं A तथा B का औसत 20, B तथा C का औसत 19 और C तथा A का औसत 21 है। A का मान क्या है?
View SolutionIf 7129p465 is divisible by 9, then the value of p is:
यदि 7129p465 , 9 से विभाज्य है, तो p का मान है:
View SolutionThe average of a, b and c is 9. The average of b and c is 10. What is the value of a?
a, b तथा c का औसत 9 है | b तथा c का औसत 10 है | a का मान कितना है ?
View SolutionA sum of Rs. x is divided among A , B and C such that the ratio of shares of A and B is 7: 12 and that of B and C 1s 8: 5. If the difference in the shares of A and C is Rs. 214 , then the value of x is:
x रुपये की राशि A , B और C में इस प्रकार विभाजित की जाती है कि A और B के हिस्से का अनुपात 7 : 12 है और B तथा C के हिस्से का अनुपात 8 : 5 है | यदि A और C के हिस्सों में 214 रुपये का अंतर है, तो x का मान ज्ञात करें |
View SolutionA sum of Rs. x is divided among A, B and C such that the ratio of the shares of A and B is 6:7 and that of B and C is 3:2. If the difference between the shares of A and C is Rs. 540, then the value of x is :
x रुपये की राशि A, B और C में इस प्रकार विभाजित की जाती है कि A और B के हिस्सों का अनुपात 6 : 7 है तथा B और C के हिस्सों का अनुपात 3 :2 है | यदि A और C के हिस्सों में 540 रुपये का अंतर है, तो x का मान क्या होगा ?
View SolutionA sum is divided among A, B, C and D such that the ratio of shares of A and B is 2:3, that of B and C is 1:2 and that of C and D is 3:4. If the difference between the shares of A and D is Rs. 648, then the sum of their shares is :
एक राशि A, B, C और D में इस प्रकार विभाजित की जाती है कि A और B के हिस्सों का अनुपात 2 : 3 है तथा B और C के हिस्सों का अनुपात 1: 2 है और C एवं D के हिस्सों का अनुपात 3 : 4 है| यदि A और D के हिस्सों में 648 रुपये का अंतर है, तो उनके हिस्सों का योग ज्ञात करें |
View SolutionA sum of Rs. 5200 is divided amongst A, B, C and D such that the ratio of shares of A and B is 2:3, that of B and C is 4:5 and that of C and D is 1:2. What is the difference between the shares of B and D?
5200 रुपये की राशि A, B, C और D में इस प्रकार विभाजित की जाती है कि A और B के हिस्सों का अनुपात 2: 3 है, B और C के हिस्सों का अनुपात 4 : 5 है तथा C और D के हिस्सों का अनुपात 1 : 2 है | B और D के हिस्सों में क्या अंतर है ?
View Solution
