जिस प्रकार विज्ञान में परिशुध्द मापन आवश्यक है, उसी प्रकार अल्पविकसित विचारो तथा सामान्य प्रेक्षणों को उपयोग करने वाली राशियों के स्थूल आकलन कर सकना भी उतना ही महत्वपूर्ण है । उन उपायों को सोचिए जिनके द्वारा आप निम्नलिखित का अनुमान लगा सकते है : (जहाँ अनुमान लगाना कठिन है वहाँ राशि की उपरिसीमा पता लगाने का प्रयास कीजिए) ।
(a) मानसून की अवधि में भारत के ऊपर वर्षाधारी मेघो का कुल द्रव्यमान ।
(b) किसी हाथी का द्रव्यमान ।
(c) किसी तूफ़ान की अवधि में वायु की चाल ।
(d) आपके सिर के बालो की संख्या ।
(e) आपकी कक्षा के कमरे में वायु के अणुओ की संख्या ।
(a) यदि मानसून की अवधि में माध्य वर्षा 10 सेमी रिकॉर्ड होती है ।
अर्थात माध्य वर्षा की ऊँचाई h = 10 सेमी = 0.1 मीटर
भारत का क्षेत्रफल सरकारी सूत्रों से प्राप्त सुचना
A = 3.3 मिलियन वर्ग किमी
=3.3×106(किमी)2
=3.3×106(103मीटर)2
=3.3×1012मीटर2
वर्षा के जल का कुल आयतन = क्षेत्रफल × ऊँचाई
V=A×h
=3.3×1012×0.1मीटर3
=3.3×1011मीटर3
वर्षा के जल का द्रव्यमान m = आयतन × घनत्व = V × d
=3.3×1011×1×103 किग्रा
=3.3×1014 किग्रा |
(b) किसी हाथी के द्रव्यमान को ज्ञात करने के लिए हम तैरने के सिध्दांत का उपयोग कर सकते हैं । किसी वस्तु का द्रव्यमान उस वस्तु द्वारा हटाए गए द्रव के भार के बराबर होता है ।
उदाहरण के लिए, जब एक नाव को जल में ले जाते हैं तो जल में नाव के डूबे हुए भाग की गहराई h1 माप लेते हैं ।
नाव द्वारा विस्थापित जल का आयतन V1=Ah1
अब हाथी को नाव पर ले जाते हैं तथा नाव के जल में डूबे भाग की गहराई h2 माप लेते हैं ।
नाव तथा हाथी द्वारा विस्थापित जल का आयतन V2=Ah2
हाथी द्वारा विस्थापित जल का आयतन, V=V2−V1
यदि जल का घनत्व d हो, तो हाथी का द्रव्यमान = हाथी द्वारा विस्थापित जल का द्रव्यमान M = V × d
=A(h2−h1)d.
(c) तूफ़ान की अवधि में आयु की चाल ज्ञात करने के लिए गैस से भरे गुब्बारे को h ऊँचाई पर ऊधर्वाधर स्थिति A में पकड़ते हैं । अब गुब्बारे को हाथ से अचानक छोड़ देते हैं जिससे गुब्बारे वायु चलने की दिशा में गति करता है । यदि गुब्बारा एक सेकण्ड में स्थिति B में पहुँच जाता है, 1 सेकण्ड में गुब्बारे द्वारा क्षैतिज दूरी d तय होती है । जबकि
∠AOB=θ
यहाँ tanθ=dh
d=htanθ
यदि θ=45∘, तो tan45∘=1
तब d = h
यहाँ d गुब्बारे द्वारा 1 सेकण्ड में चली गई दूरी है, यही वायु की चाल है ।
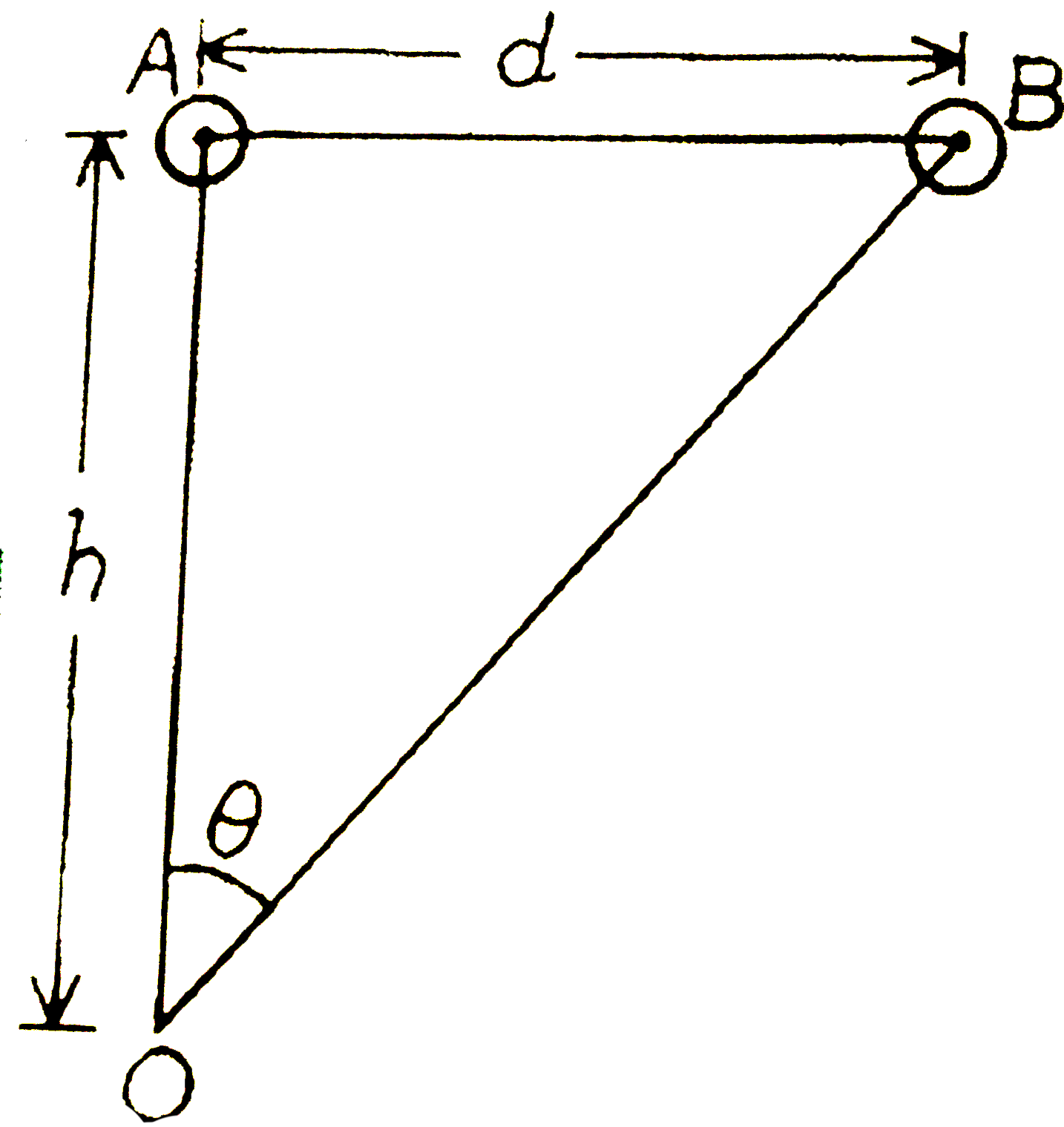
(d) सिर के बालो की संख्या ज्ञात करने के लिए यह मान लीजिए की बालो का सिर पर वितरण एकसमान है ।
सिर पर बालो की संख्या
=सिर का संपूर्ण क्षेत्रफलएक बाल के अनुप्रस्थ काट का क्षेत्रफल
यदि एक बाल की मोटाई d हो ।
बाल के अनुप्रस्थ काट का क्षेत्रफल =πr2
यहाँ r=d2
अत: A=π(d2)2=πd24
यदि मनुष्य के सिर की औसत त्रिज्या R हो ।
सिर का सम्पूर्ण क्षेत्रफल =πR2
सिर पर बालो की संख्या =πR2(πd24)=4πR2πd2=4R2d2
उदाहरण के लिए, बाल की मोटाई (d)=3×10−3 सेमी
यदि सिर की औसत त्रिज्या (R) = 9 सेमी
बालो की संख्या =4×(9)2(3×10−3)2=4×819×10−6
=36×106=3.6×107.
(e) किसी कक्षा के कमरे में उपस्थित अणुओ की संख्या ज्ञात करने के लिए कमरे के आयतन की आवश्यकता होती है । उदाहरण के लिए, यदि कक्षा के कमरे की भीतरी लम्बाई (l), चौड़ाई (b) तथा ऊँचाई (h) है ।
कक्षा के कमरे का आयतन V=l×b×hमी3 है ।
हम जानते हैं कि NTP पर एक मोल वायु का आयतन 22.4 लीटर होता है (1 लीटर =10−3मीटर3)|
अत: 1 मोल वायु का आयतन =22.4×10−3मीटर3
वायु के एक मोल में अणुओ कि संख्या = आवोगाद्रो संख्या (N)
यहाँ N=6.023×1023
अत: कक्षा के कमरे में वायु के अणुओ के संख्या
n=(6.023×1023)×(l×b×h)22.4×10−3
यदि कक्षा के कमरे कि l = 8 मीटर, b = 6 मीटर तथा h = 4 मीटर तब,
n=6.023×1023×8×6×422.4×10−3
=6.023×192×102622.4
=1156.416×102622.4
=51.626×1026
=5.16×1027
Topper's Solved these Questions
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - अतिरिक्त प्रश्न
9 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
9 Videos
- मात्रक, मापन तथा त्रुटि विश्लेषण BOOK - NOOTAN HINDICHAPTER - मात्रक, मापन तथा त्रुटि विश्लेषण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
19 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
Similar Questions
वर्षा के समय में कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है । उसे अपने छाते को टेढ़ा करके उर्ध्व के साथ θ कोण बनाना पड़ता है । कोई विद्यार्थी कोण θ व v के बीच निम्नलिखित संबंध व्युतपन्न करता है :
tanθ=v,
और वह इस संबंध के औचित्य की सिमा पता लगाता है, जैसी की आशा की जाती है यदि v → 0 तो θ→0 | (हम यह मान रहे हैं की तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा उर्ध्वाधरत: पद रही है) । क्या आप सोचते हैं की यह संबंध सही हो सकता है ? यदि ऐसा नहीं है तो सही संबंध का अनुमान लगाइए ।
View Solutionदूरी z के साथ दाब P का विचरण, P=αβe−az/kθ से व्यक्त किया जाता है, जहाँ α,β नियतांक हैं, k बोल्ट्समान नियतांक तथा θ ताप है । β का विमीय सूत्र होगा :
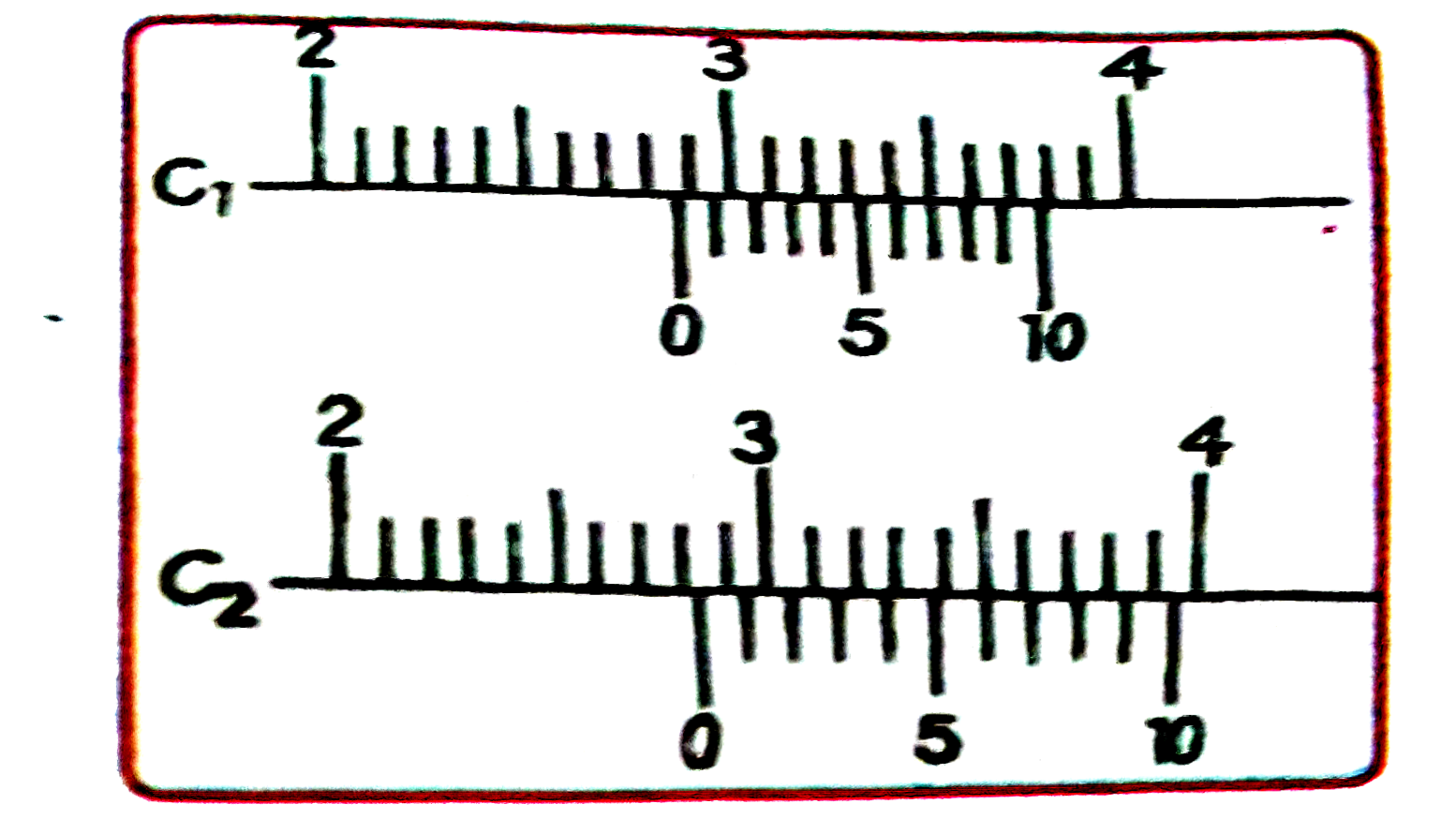
View Solutionदो वर्नियर कैलिपर्स इस तरह से हैं कि उनके मुख्य पैमाने का 1 समी, 10 समभागों में विभाजित है। एक कैलिपर (C1) के वर्नियर पमाने पर 10 बराबर भाग हैं जो कि मुख्य पैमा के 9 भागों के बराबर है। दूसरे कैलिपर (C2) के वर्नियर पैमाने पर भी 10 बराबर भाग हैं जो कि मुख्य पैमाने के 11 भागों के बराबर हैं। दोनों कैलिपर्स के पठनों को चित्र में दर्शाया गया है। C1 तथा C2 द्वारा मापे गए सही मान (सेमी में) क्रमश: हैं :
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न का अनुकूलतम है निम्नलिखित शीर्ष पर है|
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
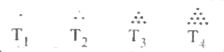
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solution. किसी तथ्य की जानकारी हेतु प्रारंभिक प्राप्त प्रेक्षणों को किस प्रकार का आँकड़ा कहा जाता है?
View Solutionप्रत्येक राष्ट्र की अपनी सांस्कृतिक धरोहर होती है जिसके बल पर वह प्रगति के पथ पर अग्रसर होता रहता है। मानव युग-युग से अपने जीवन को अधिक सुखमय, उपयोगी, शांतिमय और आनन्दपूर्ण बनाने का प्रयास कर रहा है। इस प्रयास का आधार वह सांस्कृतिक धरोहर होती है जो प्रत्येक मानव को विरासत के रूप में मिलती है. और इस प्रयास के फलस्वरूप मानव अपना विकास करता है। यह विकास सांस्कृतिक आधार के बिना संभव नहीं है। सभ्यता और संस्कृति दो अलग-अलग चीजें हैं। यद्यपि दोनों में गहरा रिश्ता है किन्तु संस्कृति मनुष्य को श्रेष्ठ और उन्नत बनाने की साधनाओं का नाम है और सभ्यता उन साधनाओं के फलस्वरूप उपलब्ध हुई जीवन प्रणाली का नाम है। सभ्यता के अन्तर में बहने वाली विचारधारा को हम संस्कृति कहते हैं जिसमें युगों से मानव-विकास के बीज विद्यमान हैं। किसी राष्ट्र का मूल्यांकन हम उसकी संस्कृति के आधार पर भी कर सकते हैं।
संस्कृति मनुष्य को श्रेष्ठ और_______ बनाने की साधनाओं का नाम है।
View Solutionकिस प्रकार का प्रश्न प्राथमिक बच्चों की भाषायी क्षमता का आकलन करने में सर्वाधिक सक्षम है?
View Solutionगैब्रिएल थेलिमाइड संश्लेषण का उपयोग, निम्नलिखित में से किसके द्वारा ऐमीन को तैयार करने के लिए किया जा सकता है?
View Solutionएमाइड को एमीन में परिवर्तित करने के लिए किस अभिक्रिया का उपयोग किया जाता है?
View Solutionयदि अभिक्रिया की मानक गिब्स मुक्त ऊर्जा (ΔrG∘) ज्ञात हो, तो निम्नलिखित में से कौन अभिक्रिया की दर का अनुमान लगाने में मदद कर सकता है?
View Solutionप्रोटीन की द्वितीयक संरचना को बनाए रखने में सबसे महत्वपूर्ण बंध का प्रकार है :
View Solutionप्रत्येक भाषा की पृष्ठभूमि में अव्यवस्थित भाषिक-व्यवस्था ही और कार्यक्रमों को गढ़ती है तथा व्यक्ति के मानसिक क्रियाकलाप के लिए निर्देशन का कार्य करती है।
View Solutionछात्र की सहायता करना अत्यावश्यक है कि उसका मन वैज्ञानिक, स्पष्ट, निश्चित और सूक्ष्मता से सोचने वाला तथा उसके साथ ही साथ मन की गहराईयों को अनावृत करने वाला हो। क्या छात्र को इस प्रकार शिक्षित करना संभव है कि वह सभी लेबिलों के परे जो कर सके तथा उस वस्त का पता लगा सके, उसका अनुभव कर सके, जिसको मन नहीं माप सकता, जो किसी पुस्तक में नहीं लिखा है। यदि इस प्रकार के एक विद्यालय में ऐसी शिक्षा संभव हो सके, तो वह अनूठी होगी। आप सभी को यह देखना चाहिए कि इस प्रकार के विद्यालय का निर्माण कितना मूल्यवान होगा। केवल नृत्य, संगीत, गणित और दूसरे पाठों पर ध्यान देना समस्त जीवन नहीं है। शांत बैठना तथा अपने को देखना, सूक्ष्म दृष्टि प्राप्त करना, अवलोकन करना भी जीवन का अंग है। विचार कैसे किया जाए. किस पर विचार किया जाए, तथा आप विचार क्यों कर रहे हैं, इसको देखना भी आवश्यक है।
लेखक की दृष्टि में सर्वाधिक महत्वपूर्ण क्या है?
View Solution
