चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि
ar(APB)×ar(CPD)=ar(APD)×ar(BPC)
Step by step video & image solution for चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि "ar"(APB)xx"ar"(CPD)="ar"(APD)xx"ar"(BPC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - MANOHAR RAYCHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9 (C)
4 Videos
- संख्या पद्धतिBOOK - MANOHAR RAYCHAPTER - संख्या पद्धतिEXERCISE - प्रश्नावली 1(J)
17 Videos
- सांखियकीBOOK - MANOHAR RAYCHAPTER - सांखियकीEXERCISE - प्रश्नावली 14 (H)
14 Videos
Similar Questions
एक चतुर्भुज ABCD का BD एक विकर्ण है। भुजा BD पर AM तथा CN डालें गये लम्ब है। सिद्ध कीजिए कि
क्षेत्रफल (ABCD)=12BD(AM+CN)

View Solutionनिम्नलिखित में से परिमेय संख्याएं छांटकर लिखिएः
√3,π3,227,3√4,√414 और 2.33
View Solution5, 9, 2, 5, 4, 5, 2 का बहुलक ज्ञात कीजिए ।
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
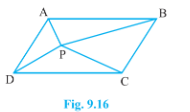
View SolutionDiagonals AC and BD of square ABCD intersect each other at point P. Show that ar(/_APB)xx ar(/_CPD)=ar(/_APD)xx ar(/_BPC)
View Solutionआकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(APB)+ar(PCD)=12ar(ABCD)
(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु P पर प्रतिच्छेद करते है दर्शाइए कि ar(APB)×ar(CPD)=ar(APD)×ar(BPC) है ।
View Solutionदिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है |दर्शाइए की
(i)ar(APB)+ar(PCD)=12ar(ABCD)
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि ar(APB)×ar(CPD)=ar(APD)×ar(BPC) है।
संकेत : A और C से BD पर लम्ब खींचिए
View SolutionIn P is a point in the interior of a parallelogram ABCD. Show that<br>(ii)ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
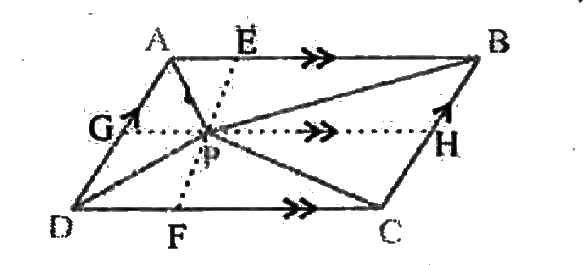
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPD).
[Hint : From A and C, draw perpendiculars to BD.
View SolutionIN the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = 12 ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)
View SolutionDiagonals AC and BD of a quadrilateral ABCD each other at P. Show that ar (APB) × ar (CPD) =ar (APD) × ar (BPC)
View SolutionIn the given figure, P is any point located in the interior of the parallelogram ABCD. Indicate that (i) ar (Delta APB ) + ar (Delta PCD ) = (1)/(2) (ar||^(g m)ABCD) (Ii) ar(Delta APD) + ar(Delta BPC ) = ar(Delta APB) + ar(Delta PCD)
View SolutionDiagonals AC and BD of quadrilateral ABCD intersect each other at P. Show that ar (APB)×ar(CPD) = ar (APD)×ar(BPC).
View Solution
