Diagonals AC and BD of □ABCD intersect each other at point P. Show that ar(△APB)×ar(△CPD)=ar(△APD)×ar(△BPC)
AM⊥BD&CN⊥BD
L.H.S.=area(∠APB)×area(∠CPD)
=12×(BP×AM)×12(PD×CN)
=12(BP×CN)×12(PD×AM)
=area(∠BPC)×area(∠APD)
L.H.S=R.H.S
Similar Questions
Diagonals AC and BD of □ABCD intersect each other at point P. Show that ar(△APB)×ar(△CPD)=ar(△APD)×ar(△BPC)
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
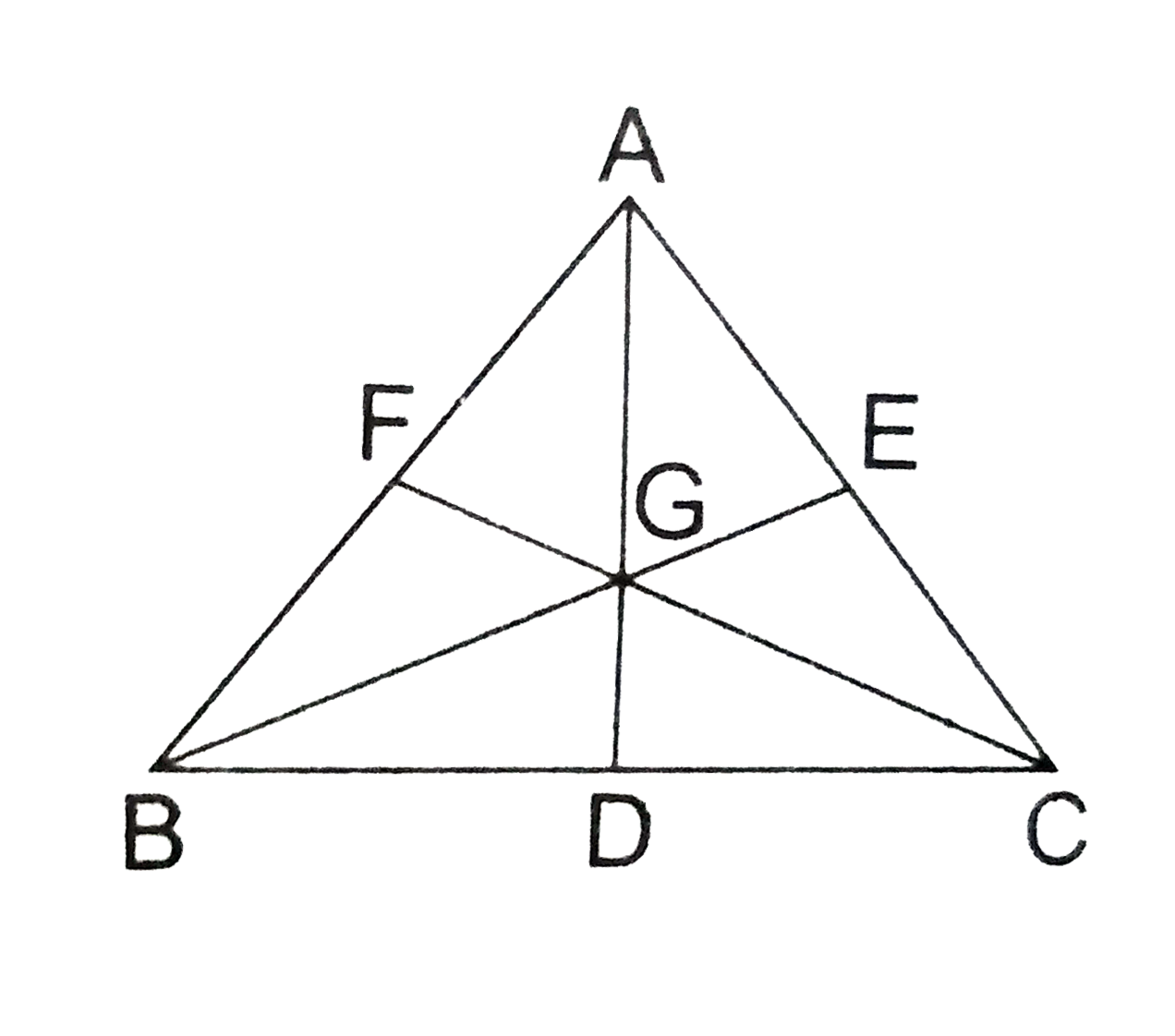
View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
View SolutionDiagonals AC and BD of a trapezium ABCD with AB∣∣CD intersect each other at O. Prove that ar (△AOD)=ar(△BOC).
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
View SolutionIn the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that

ar(ΔDOC) = ar(ΔAOB)
View SolutionDiagonal PR and QS of quadrilateral PQRS intersects at T such that PT= TR and PS= QR, show that ar (ΔPTS)= ar (ΔRTQ)
View SolutionThe diagonals AC and BD of a quadrilateral ABCD intersect at point 'O'. If BO = OD, then prove that the areas of ΔABCandΔADC are equal
View Solution
