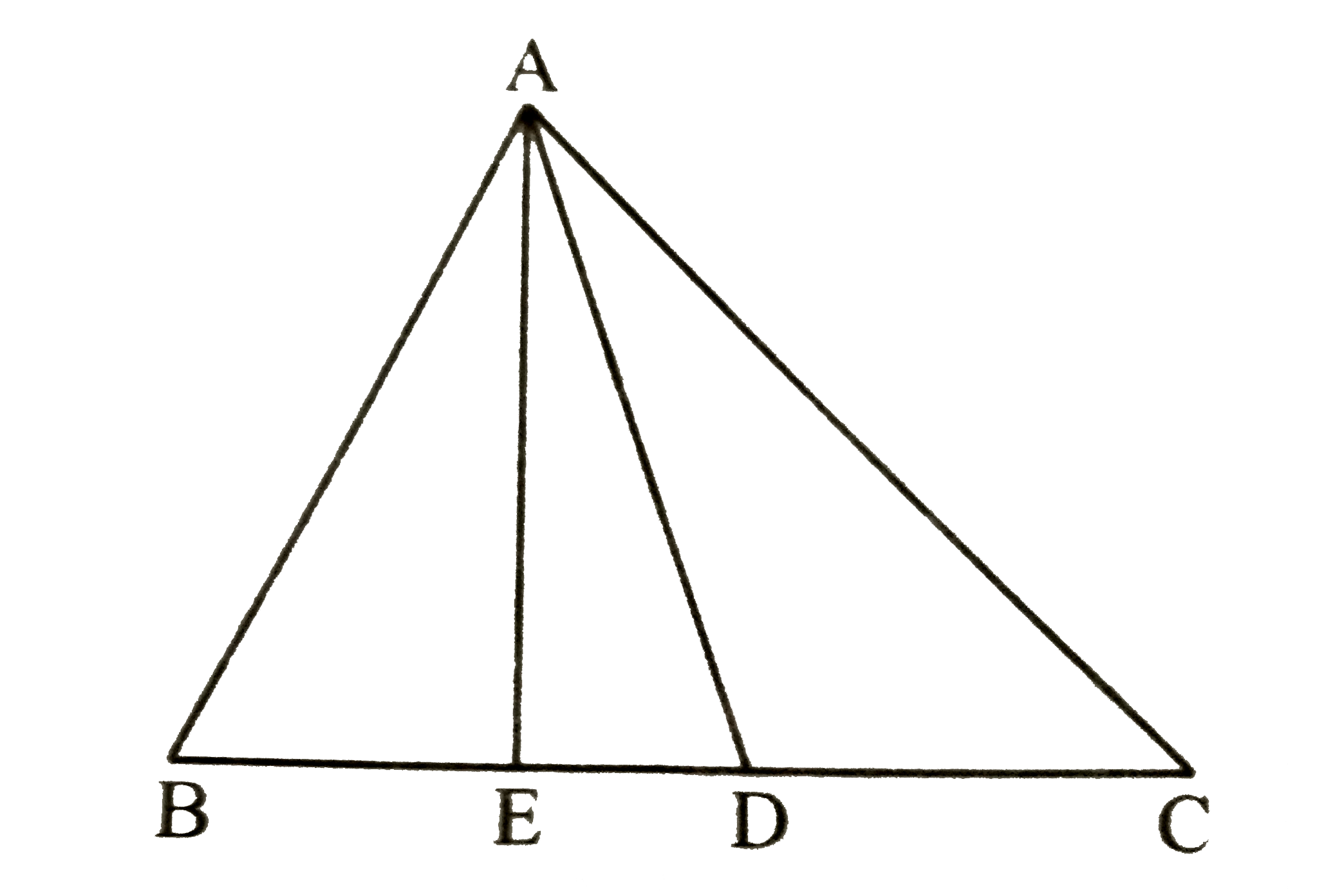
एक △ABC में, AC>BD है | D, BC का मध्य बिन्दु है तथा AE⊥BC तो सिद्ध कीजिए कि :
(i) AC2=AD2+BC⋅DE+14BC2
(ii) AB2=AD2−BC⋅DE+14BC2
स्पष्ट्तः यहाँ, ∠AED=90∘
इसलिए, ∠ADE<90∘ तथा ∠ADC>90∘
(i) △ADC में, ∠ADC एक अधिक कोण है |
इसलिए,
AC2=AD2+2DC⋅DE
=AD2+(12BC)2+2⋅12BC⋅DE
=AD2+14BC2+BC⋅DE
=AD2+BC⋅DE+14BC2
(ii) अब △ABD में, ∠ADE एक न्यून कोण है | तब
AB2+AD2+BD2−2BD⋅DE
इसलिए, AB2=AD2+(12BC)2−2⋅12BC⋅DE=AD2+14BC2−BC⋅DE
अतः AB2=AD2−BC⋅DE+14BC2
Topper's Solved these Questions
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.1
9 Videos
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.2
17 Videos
- त्रिकोणमितीय अनुपात एव असमिकाएँ BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण
35 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण
29 Videos
Similar Questions
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
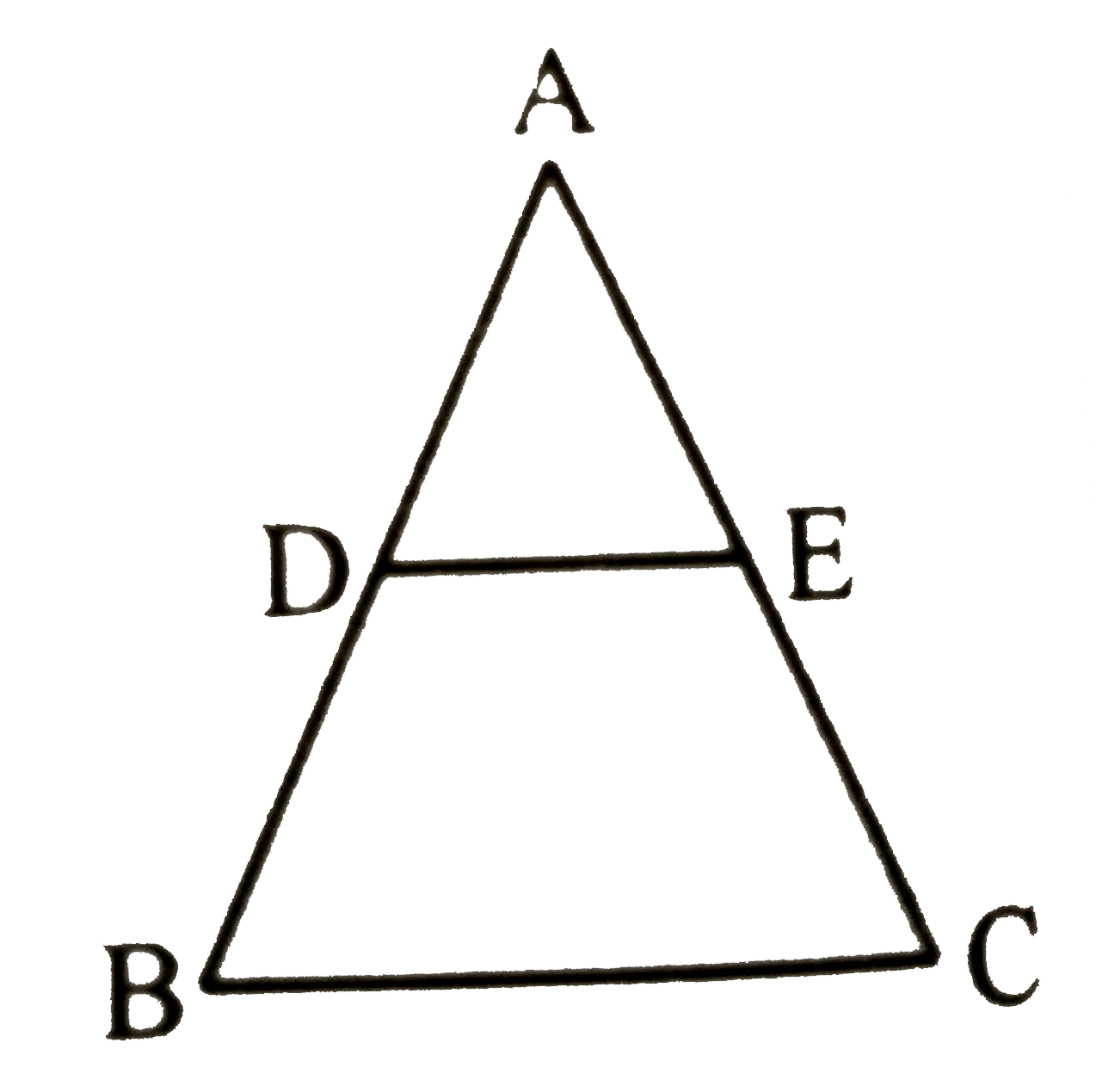
View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |

View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
View SolutionIn ABC, DE is parallel to base BC , with D on AB and E on AC . If ADDB=23 , find BCDE .
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCxDE+14BC2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View SolutionIn ΔABC,D is the midpoint of BC and AE⊥BC. If AC>AB, show that AB2=AD2−BC⋅DE+14BC2
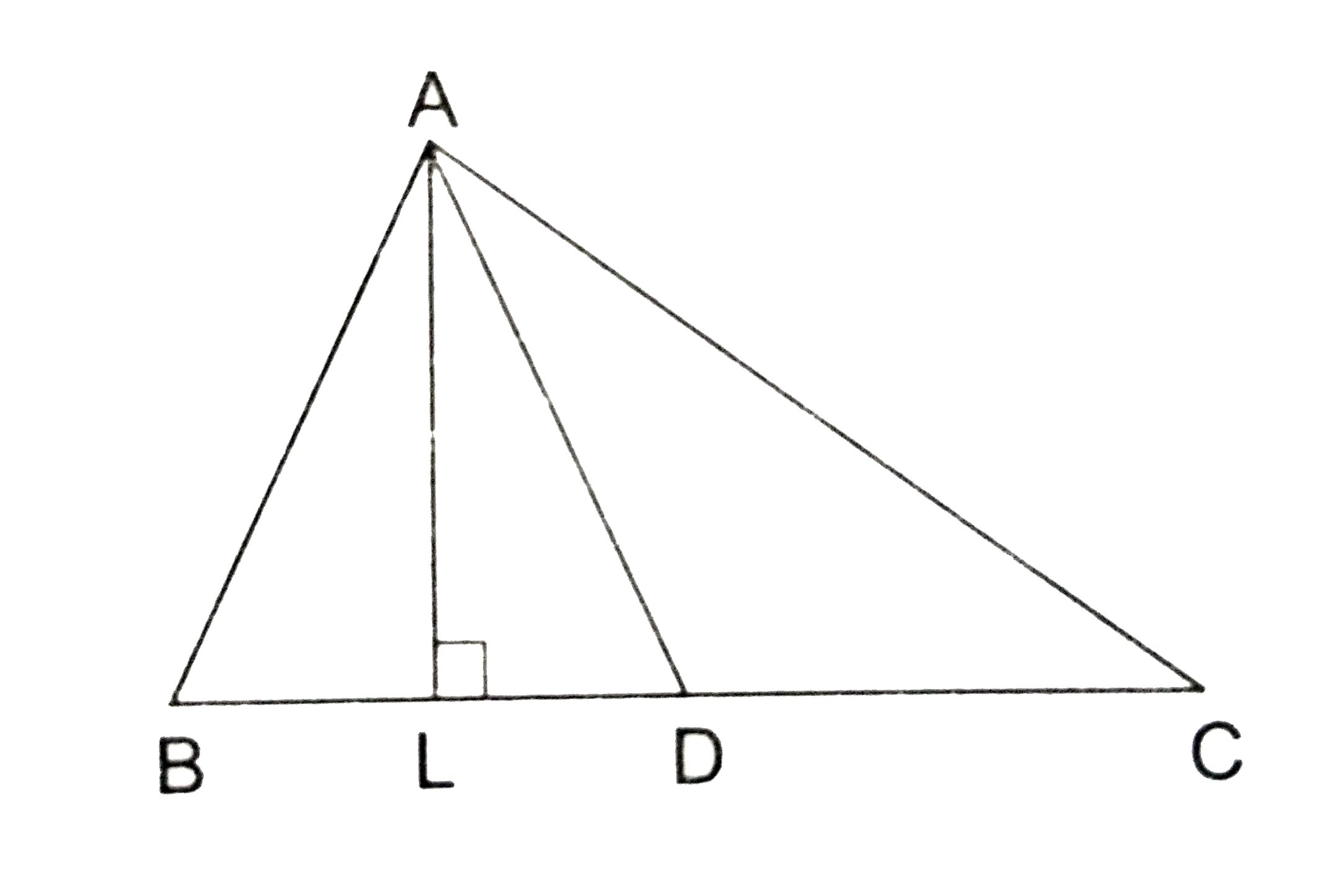
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
View Solutionसिद्ध कीजिए कि:
∣∣∣ad+bcbd−acac−bdad+bc∣∣∣=(a2+b2)(c2+d2).
View Solutionत्रिभुज ABC की भुजाओं AB तथा AC पर क्रमशः बिंदु D तथा E इस प्रकार है की DE∣∣BC है|यदि AD = 2 .4 सेमि., AE =3 .2 सेमि., DE =2 सेमि., तथा BC = 6 सेमि,हो तो BD तथा CE का मान ज्ञात करो|
View Solutionत्रिभुज ABC में D भुजा BC का मध्यबिंदु है और AE⊥BC सिद्ध कीजिए कि
(i) AC2=AD2+BC.DE+14BC2
AB2=AD2−BC.DE+14BC2
View SolutionIn a △ABC, AB = AC and AD⊥BC, then BD = .......
View SolutionIn ΔABC, BD:CD=3:1 and AD⊥BC. Prove that 2(AB2−AC2)=BC2.
View SolutionIn acute angled triangle ABC, AD is median and AE is altitude , prove that:
(i) AC2=AD2+BC×DE+14BC2
(ii) AB2=AD2−BC×DE+14BC2
(iii) AC2+AB2=2AD2+12BC2
View Solution
