In aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
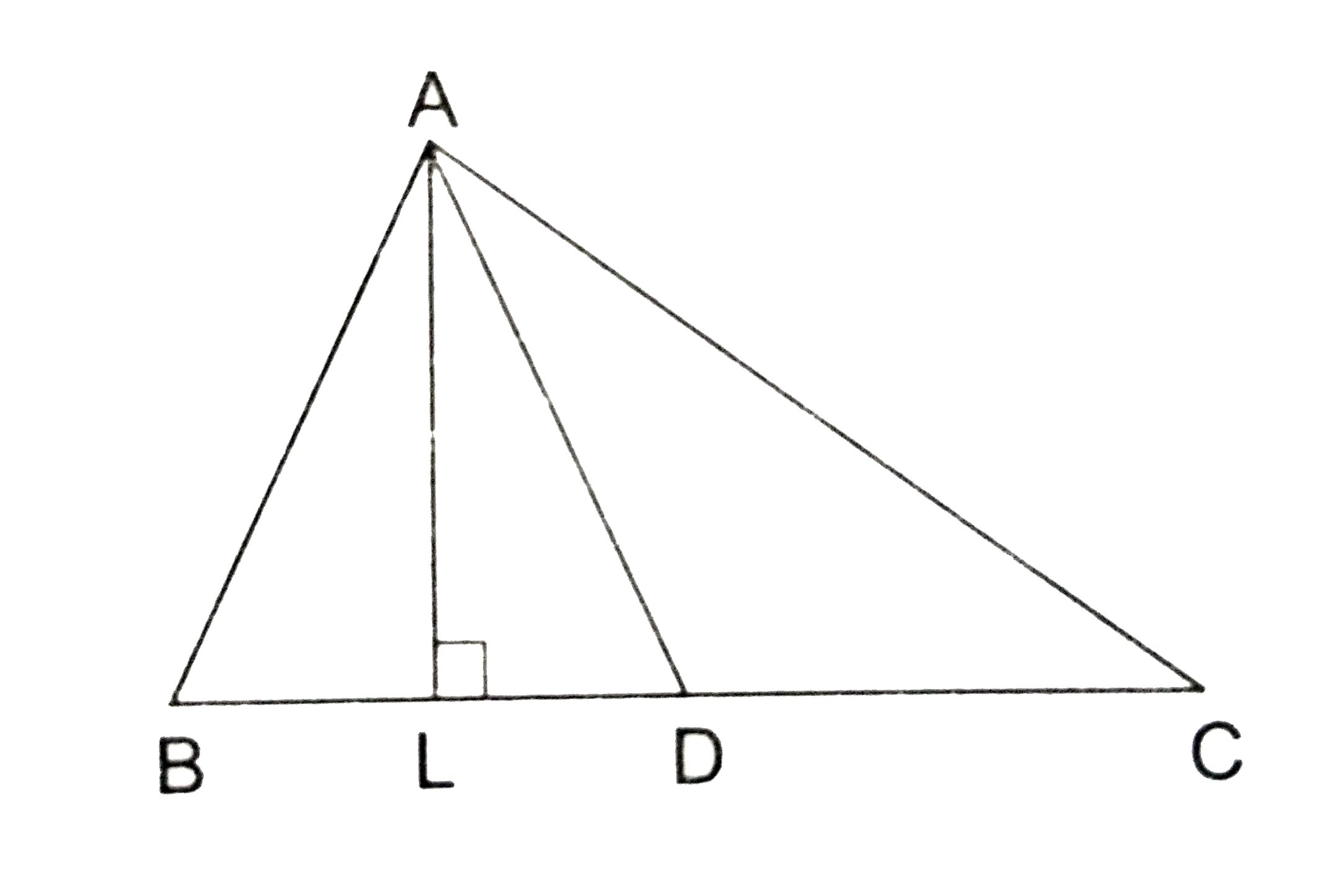
In right ΔACL,AC2=AL2+LC2 .....(i)
In right ΔALD,AL2=AD2−DL2 .....(ii)
∴AC2=(AD2−DL2)+LC2 [ from (i) and (ii) ]
=(AD2−DL2)+(DL+DC)2
=(AD2−DL2)+(DL+12BC)2
=AD2+BC⋅DL+14BC2=AD2+BC⋅DL+(BC2)2
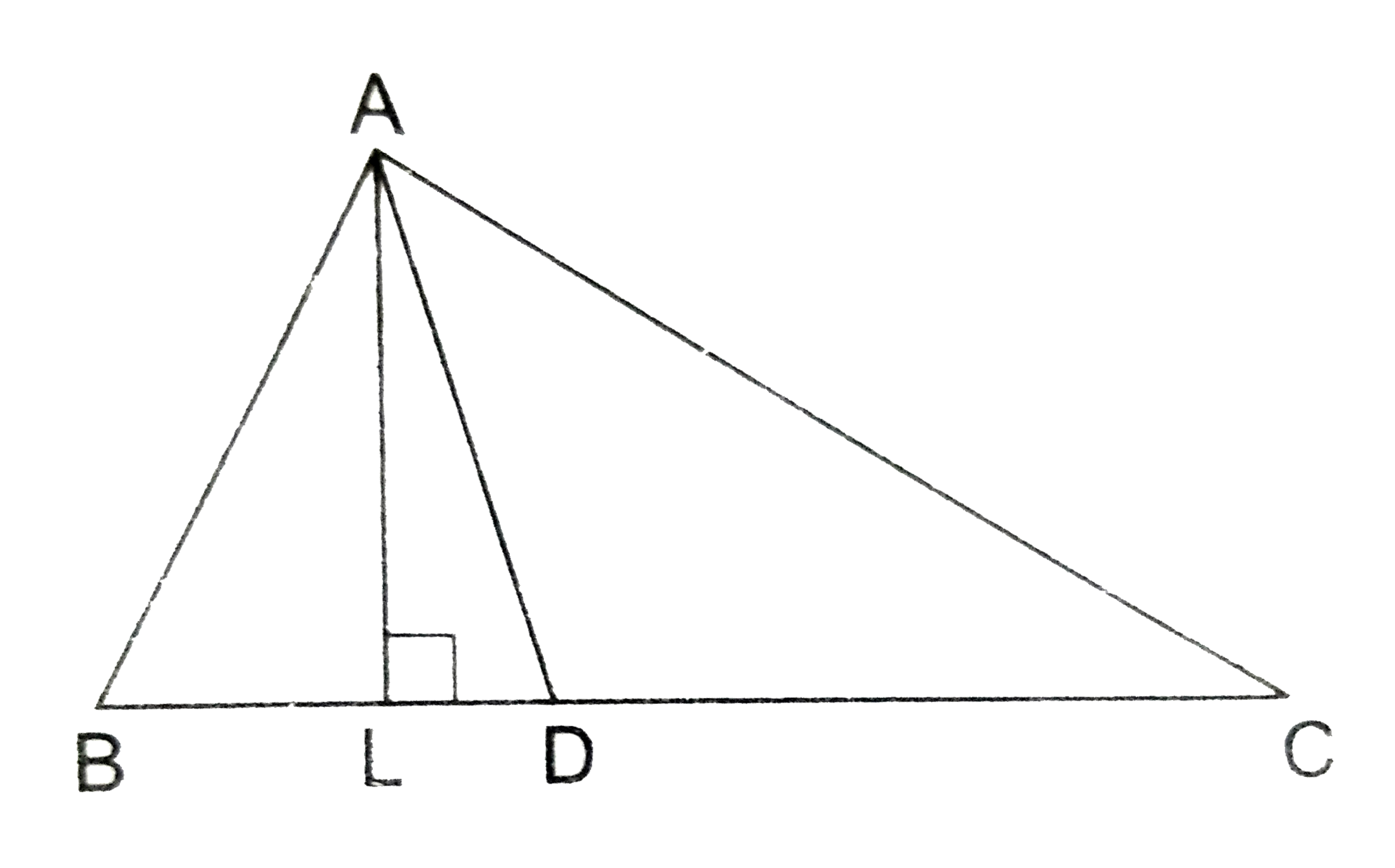
(b) In right ΔABL,AB2=AL2+LB2 .....(iii)
In right ΔALD,AL2=AD2−DL2 .....(iv)
∴AB2=(AD2−DL2)+LB2 [ from (iii) and (iv) ]
=(AD2−DL2)+(BD−DL)2
=(AD2−DL2)+(12BC−DL)2=AD2−BC⋅DL+(BC2)2
(c) Adding the results of (a) and (b), we get
AC2+AB2=2AD2+12BC2.
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7E
30 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)
53 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C
13 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Seg AD is the median of △ABC and AM⊥BC. Prove that : (i)AC2=AD2+BC×DM+(BC2)2 (ii)AB2=AD2−BC×DM+(BC2)2.
View SolutionIn a ΔABC, ∠B is an acute-angle and AD⊥BC. Prove that:
AB2+CD2=AC2+BD2
View SolutionIn ΔABC,D is the midpoint of BC and AE⊥BC. If AC>AB, show that AB2=AD2−BC⋅DE+14BC2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCxDE+14BC2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View SolutionIn an isoscles ΔABC,AB=ACandD is a point on BC. Prove that AB2−AD2=BD⋅CD.
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
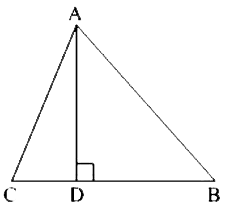
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
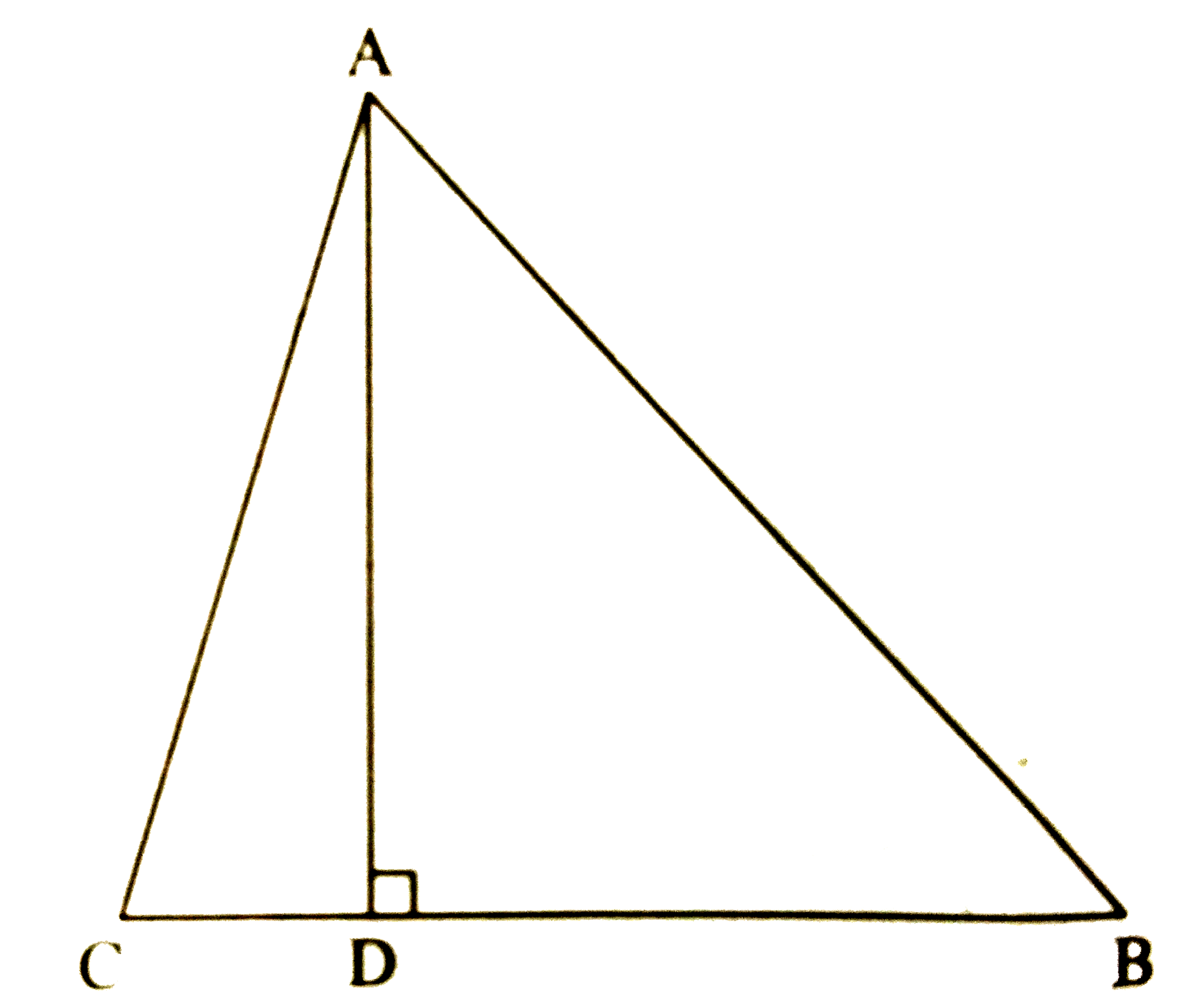
View SolutionIn ΔABC,
seg AD⊥ seg BC,
DB=3CD.
Prove that 2AB2=2AC2+BC2.
View SolutionIn a triangle ABC,B=90∘ and D is the mid-point of BC then prove that AC2=AD2+3CD2
View Solution