In a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
Step by step video & image solution for In a triangle A B C ,\ A C > A B , D is the mid-point of B C and A E_|_B C . Prove that: (i) A B^2=A D^2-B C D E+1/4B C^2 (ii) A B^2+A C^2=2\ A D^2+1/2B C^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
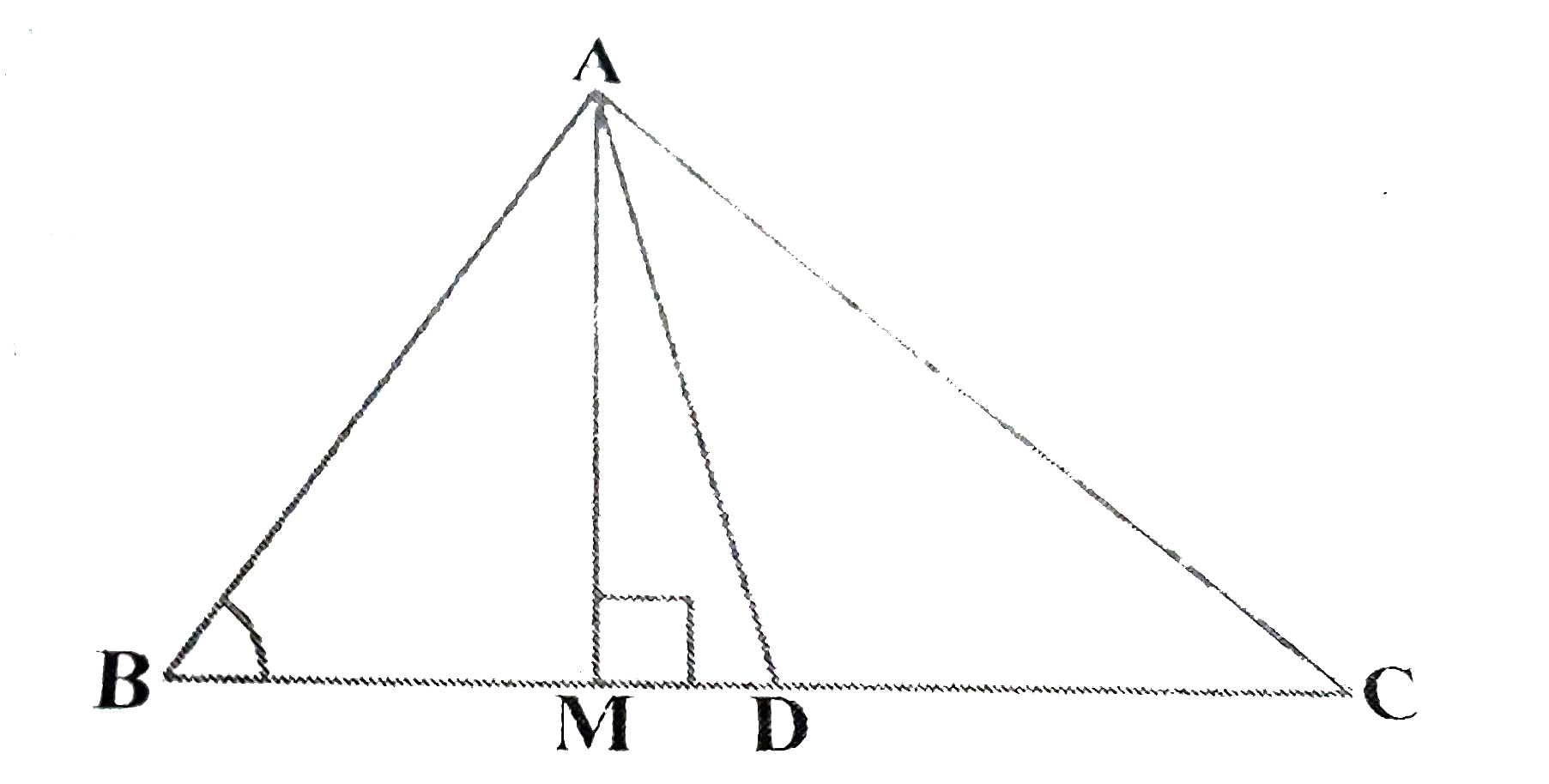
In figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
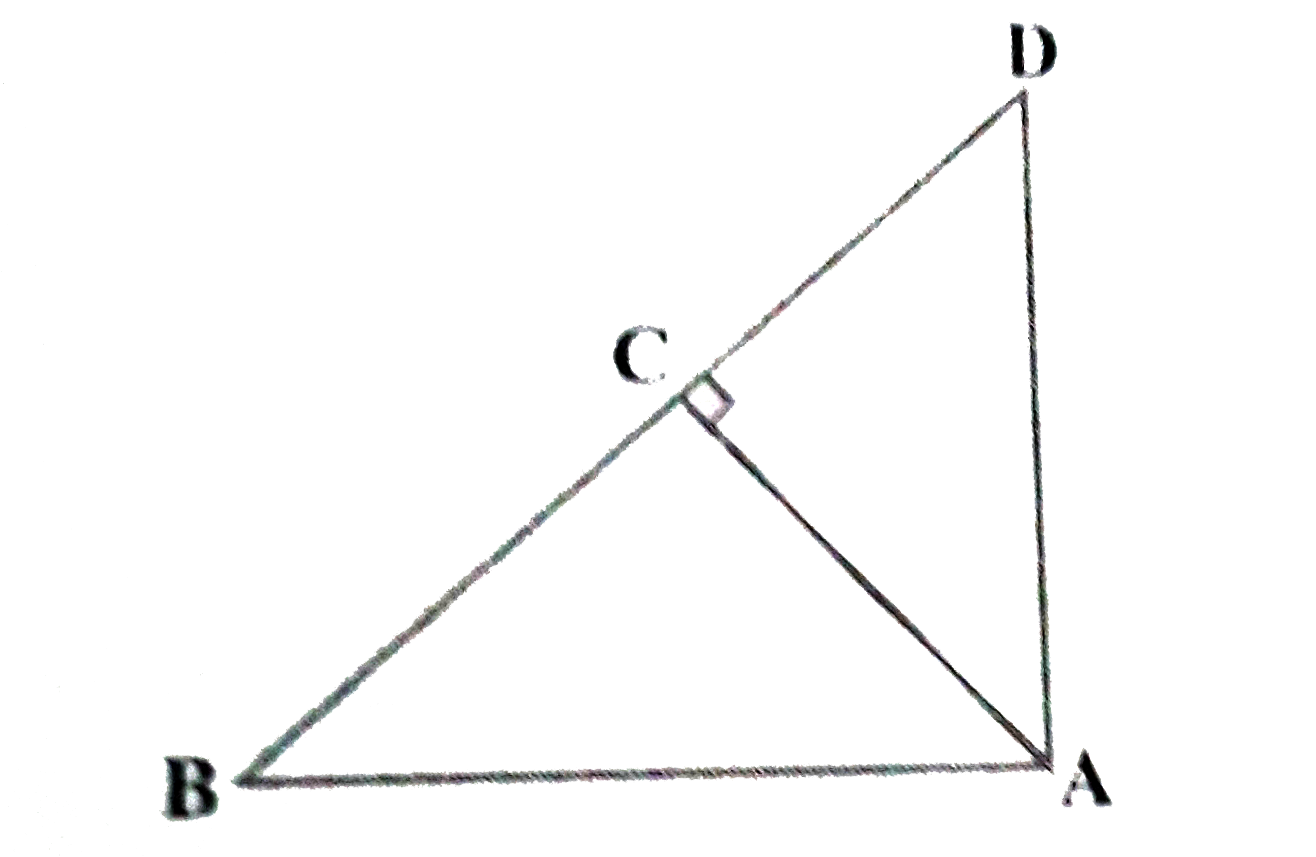
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

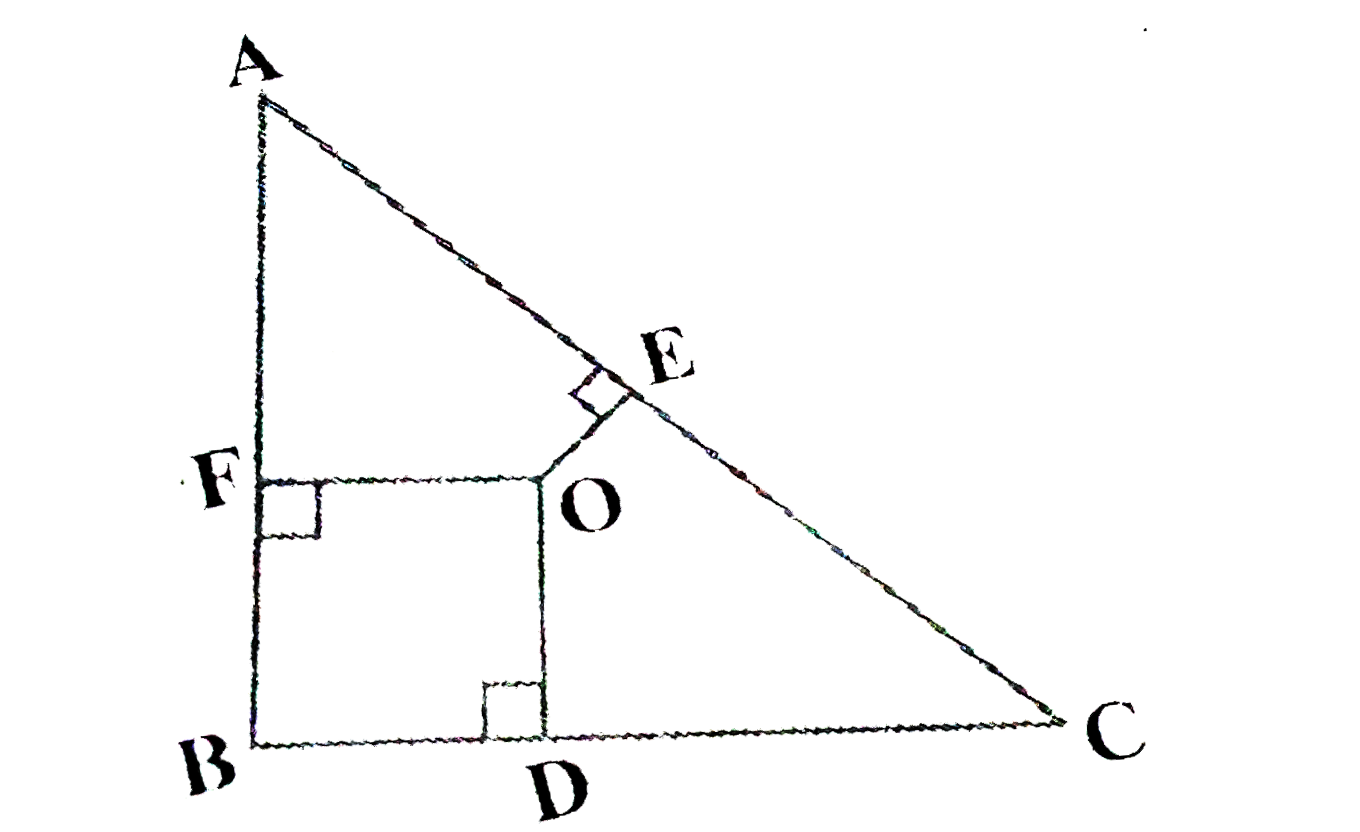
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
View SolutionABCD is a parallelogram and E is the mid-point of BC, DE and AB when produced meet at F. Then AF= 32AB (b) 2 AB (c) 3 AB (c) 54 AB
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View Solution
