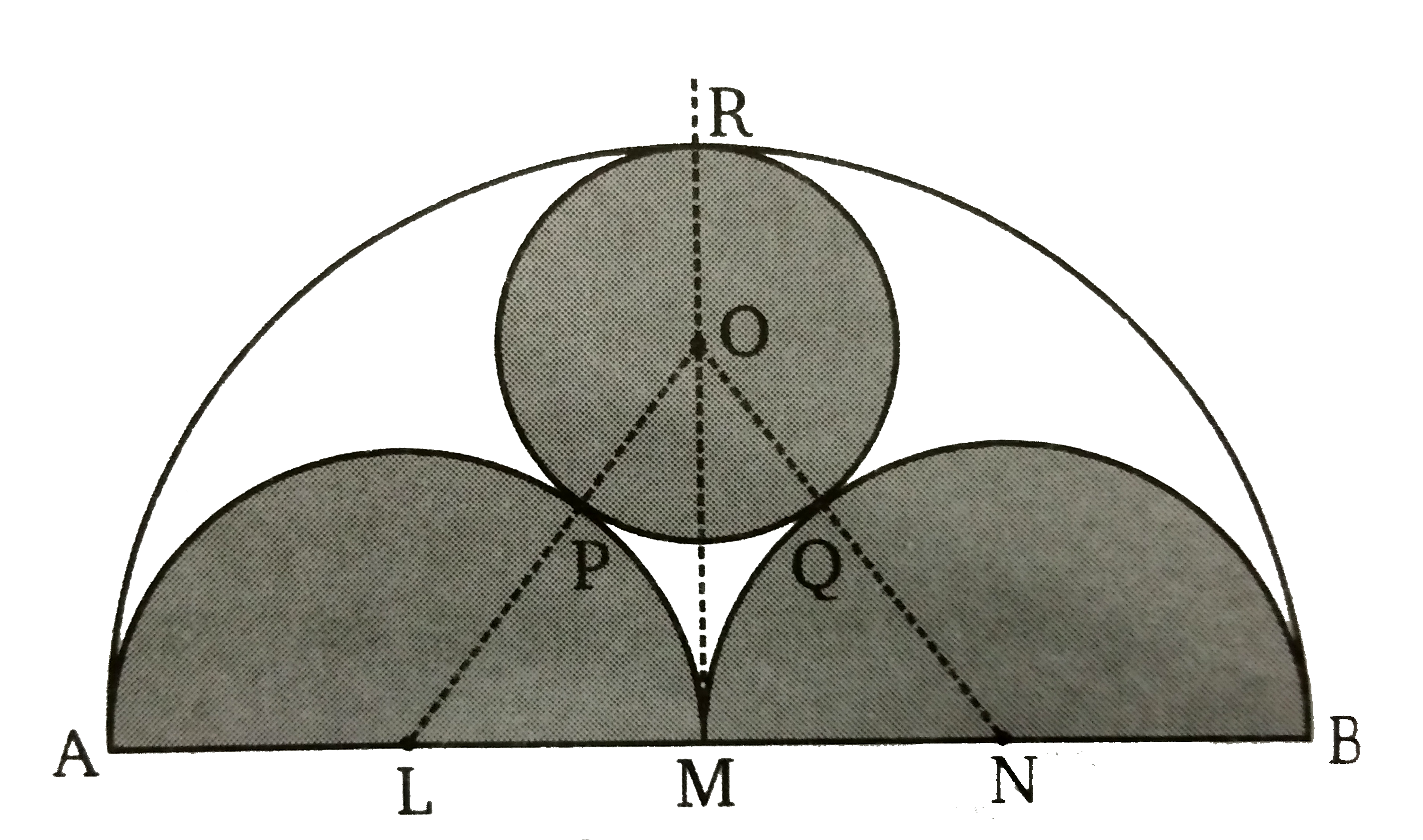
AB एक रेखाखण्ड है तथा M उसका मध्यबिंदु है। AM, MB तथा AB को व्यास मानकर रेखा AB के एक ओर अर्द्ध C(O, r) वृत्त खींचे गये हैं । एक वृत्त ऐसा खींचा गया है , जो इन tinon अर्द्ध वृतों को स्पर्श करता है। सिद्ध कीजिए कि r=16AB
यहाँ O, P, L और बिन्दु O, Q, N संरेख हैं। इसी प्रकार R, O, M संरेख हैं।
माना AB = x
∴OL=r+x4 व ON=r+x4
(∵PL=LM=x4)
∵OLN एक समद्विबाहु त्रिभुज है तथा M, आधार LN का मध्य बिन्दु है। इसलिए OM, LN पर लम्ब है।
⇒ΔOML एक समकोण त्रिभुज होगा ।
∴OL2=OM2+LM2
⇒(r+x4)2=(RM−r)2+(x4)2=(x2−r)2+(x4)2
⇒r2+rx2+x216=x24+r2−rx+x216⇒3rx2=x24
अतः r=x6=16AB
Topper's Solved these Questions
- वृत्त BOOK - BALAJI PUBLICATIONCHAPTER - वृत्त EXERCISE - अभ्यास प्रश्न 8.1 (अतिलघु उत्तरीय प्रश्न)
4 Videos
- वृत्त BOOK - BALAJI PUBLICATIONCHAPTER - वृत्त EXERCISE - अभ्यास प्रश्न 8.1 (लघु उत्तरीय प्रश्न - II)
2 Videos
- वास्तविक संख्याऐंBOOK - BALAJI PUBLICATIONCHAPTER - वास्तविक संख्याऐंEXERCISE - स्वमूल्यांकन परीक्षण
18 Videos
- वृत्तों से समबन्धित क्षेत्रफल BOOK - BALAJI PUBLICATIONCHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
Similar Questions
6 सेमी त्रिज्या के वृत्त के केन्द्र से 8 सेमी दूर स्थित एक बिंदु से खींची गई स्पर्श रेखा की लम्बाई ज्ञात कीजिये ।
View Solutionएक बिंदु A वृत्त केन्द्र से 26 सेमी दूर है तथा A से वृत्त पर स्पर्शी की लम्बाई 24 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए ।
View Solutionनिम्नलिखित संख्या-युग्मो के HCF ज्ञात कीजिए ।
(i) 156, 13
(ii) 1001, 385
(iii) 81445, 687897
View Solution6 सेमी त्रिज्या वाले वृत्त पर 60∘ पर त्रिज्यखण्ड का क्षेत्रफल व परिमाप ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View SolutionAB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then the length of BC is : AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
View SolutionPAT is a tangent to a circle at a point A on it , and AB is a chord such that, angle BAT= 72^@ . If C is a point on the circle such that angle CBA=58^@ , then what is the measure of angle CAB ? PAT एक वृत्त के बिंदु A से इस पर खींची गयी स्पर्श रेखा है तथा AB एक ऐसी जीवा है कि angle BAT= 72^@ यदि C वृत्त पर स्थित ऐसा बिंदु है कि angle CBA=58^@ है, तो angle CAB का मान ज्ञात करें |
View SolutionIn a circle with centre O, AB is a diameter. Points C, D and E are on the circle on one side of AB such that ABEDC is a pentagon. The sum of angles ACD and DEB is : केंद्र O वाले एक वृत्त में, AB एक व्यास है | बिंदु C, D तथा E AB के एक तरफ वृत्त इस प्रकार स्थित हैं कि ABEDC एक पंचभुज है | कोण ACD और DEB का योग ज्ञात करें |
View SolutionIn a circle with centre O, ABDC is a cyclic quadrilateral with AB as a diameter of the circle. AC and BD produced meet at E. If angle CED=70^@ , then what is the measure of angle COD ? केंद्र O वाले एक वृत्त में, ABDC एक चक्रीय चतुर्भुज है जिसमें AB वृत्त का व्यास है| AC और BD को बढ़ाया गया है जो E पर मिलते हैं | यदि angle CED=70^@ है, तो angle COD का मान ज्ञात करें |
View Solution
