PAT is a tangent to a circle at a point A on it , and AB is a chord such that, ∠BAT=72∘. If C is a point on the circle such that ∠CBA=58∘, then what is the measure of ∠CAB ?
PAT एक वृत्त के बिंदु A से इस पर खींची गयी स्पर्श रेखा है तथा AB एक ऐसी जीवा है कि ∠BAT=72∘ यदि C वृत्त पर स्थित ऐसा बिंदु है कि ∠CBA=58∘ है, तो ∠CAB का मान ज्ञात करें |
50∘
62∘
48∘
60∘
To find the measure of angle CAB in the given geometry problem, we can follow these steps:
Step 1: Understand the Geometry
We have a circle with a tangent line PAT at point A. The chord AB is drawn, and we know:
- Angle BAT = 72°
- Angle CBA = 58°, where C is a point on the circle.
Step 2: Identify the Angles
From the problem, we know:
- Angle BAT = 72° (the angle between the tangent and the chord).
- Angle CBA = 58° (the angle at point B formed by the chord AB and line BC).
Step 3: Use the Alternate Segment Theorem
According to the Alternate Segment Theorem, the angle formed between a tangent and a chord through the point of contact is equal to the angle in the alternate segment. Therefore:
- Angle ACB = Angle BAT = 72°.
Step 4: Apply the Triangle Angle Sum Property
In triangle ABC, we can find angle CAB using the triangle angle sum property, which states that the sum of the angles in a triangle is 180°.
Thus, we have:
Angle CAB+Angle CBA+Angle ACB=180°
Substituting the known values:
Angle CAB+58°+72°=180°
Step 5: Solve for Angle CAB
Now, we can simplify the equation:
Angle CAB+130°=180°
Subtracting 130° from both sides gives:
Angle CAB=180°−130°=50°
Final Answer
Thus, the measure of angle CAB is:
Angle CAB=50°
---
We have a circle with a tangent line PAT at point A. The chord AB is drawn, and we know:
- Angle BAT = 72°
- Angle CBA = 58°, where C is a point on the circle.
From the problem, we know:
- Angle BAT = 72° (the angle between the tangent and the chord).
- Angle CBA = 58° (the angle at point B formed by the chord AB and line BC).
According to the Alternate Segment Theorem, the angle formed between a tangent and a chord through the point of contact is equal to the angle in the alternate segment. Therefore:
- Angle ACB = Angle BAT = 72°.
In triangle ABC, we can find angle CAB using the triangle angle sum property, which states that the sum of the angles in a triangle is 180°.
Thus, we have:
Angle CAB+Angle CBA+Angle ACB=180°
Substituting the known values:
Angle CAB+58°+72°=180°
Now, we can simplify the equation:
Angle CAB+130°=180°
Subtracting 130° from both sides gives:
Angle CAB=180°−130°=50°
Thus, the measure of angle CAB is:
Angle CAB=50°
Topper's Solved these Questions
Similar Questions
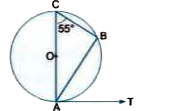
In Fig O is the centre of a circle and AT is a tangent at point A . what is the measure of ∠BAT ?
View SolutionTwo touch lines drawn from a point P outside of a circle with center O are PA and PB. A and B is the point on the circle. If ∠APB=70, then what is the value of ∠OAB ?
केंद्र O वाले एक वृत्त के बाहर किसी बिंदु P से खींची गयी दो स्पर्श रेखाएं PA और PB है | A और B वृत्त पर बिंदु है | यदि ∠APB=70, तो ∠OAB का मान क्या है ?
View Solution
Knowledge Check
AB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?A5∘B7∘C17∘D6∘
PA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that ∠APB=142∘, then ∠OAB is equal to:
PA और PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे दो बिंदु हैं कि ∠APB=142∘ है, तो ∠OAB का मान ज्ञात करे
View SolutionIn a circle with centre O, PQR is a tangent at the point Q on it. AB is a chord in the circle parallel to the tangent such that ∠BQR=70∘. What is the measure of ∠AQB ?
केंद्र O वाले एक वत्त में, PQR इस पर स्थित बिंदु Q पर एक स्पर्श रेखा है | AB वृत्त में एक जीवा है जो स्पर्श रेखा से इस प्रकार समानांतर है कि ∠BQR=70∘ है | ∠AQB का मान ज्ञात करें |
View SolutionO is the centre of a circle to which PAX and PBY are tangents from a point P at points A and B. Q is a point on the circle ,such that ∠QAX=49∘, and ∠QBY=62∘ .What is the measure of ∠AQB ?
O एक वृत्त का केंद्र है जिस पर PAX और PBY स्पर्श रेखाएं हैं जो बिंदु P से A और B पर खींची गयी हैं | Q, वृत्त पर स्थित एक बिंदु है जो इस प्रकार है कि ∠QAX=49∘, और ∠QBY=62∘ है | ∠AQB का मान क्या है ?
View SolutionPA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that ∠APB=80∘, then ∠OAB is equal to:
PA और PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे दो बिंदु हैं कि ∠APB=80∘ है, तो ∠OAB का मान क्या होगा ?
View SolutionPA and PB are the tangents to a circle with centre O, from a point P outside the circle. A and B are the points on the circle. If ∠APB=72∘,then ∠OAB is equal to:
PA तथा PB एक वृत्त पर वृत्त के बाहर स्थित बिंदु P से खींची गयी स्पर्श रेखाएं हैं जिसका केंद्र O है | A तथा B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=72∘ है, तो ∠OAB का मान ज्ञात करें |
View SolutionPAQ is a tangent to a circle with centre O, at a point A on it. AB is a chord such that ∠BAQ=x∘ (x<90). C is a point on the major arc AB such that ∠ACB=y∘. If ∠ABO=32∘, then the value of x+y is:
PAQ केंद्र O वाले एक वृत्त पर स्थित बिंदु A से जाने वाली स्पर्श रेखा है | AB एक ऐसी जीवा है कि ∠BAQ=x∘ (x<90) है | C बड़ी चाप AB पर स्थित एक ऐसा बिंदु है कि ∠ACB=y∘ है | यदि ∠ABO=32∘ है, तो x+y का मान क्या होगा ?
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If ∠APB=40∘, then ∠OAB is equal to:
PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=40∘ है, तो ∠OAB का मान ज्ञात करें |
View Solution