AB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then
the length of BC is :
AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
2√5cm
6√6cm
2√6cm
6√5cm
To find the length of BC in the given circle problem, we can follow these steps:
Step 1: Understand the Geometry
We have a circle with center O, diameter AB, and a tangent CB at point B. The line AC intersects the circle at point G. We know the radius of the circle (r) is 6 cm, and the length AG is 8 cm.
Step 2: Determine the Diameter
Since the radius is 6 cm, the diameter AB can be calculated as:
AB=2×r=2×6=12 cm
Step 3: Set Up the Right Triangle
Using the property that the radius is perpendicular to the tangent at the point of tangency (point B), we can form a right triangle OBC, where:
- OB = radius = 6 cm
- BC = length we want to find (let's denote it as y)
- OC = length from the center O to point C
Step 4: Apply the Pythagorean Theorem
In triangle OBC, we can apply the Pythagorean theorem:
OB2+BC2=OC2
Substituting the known values:
62+y2=OC2
36+y2=OC2(1)
Step 5: Find Length OC
Next, we need to find OC. Since AG = 8 cm and G lies on the circle, we can express OC in terms of AG and CG. Let CG be x, then:
AC=AG+GC=8+x
Using the power of a point theorem, we have:
CB2=AG⋅AC
Substituting the known values:
y2=8⋅(8+x)
y2=64+8x(2)
Step 6: Solve the Equations
Now we have two equations:
1. 36+y2=OC2
2. y2=64+8x
From (1), we can express OC in terms of y:
OC2=36+y2
Substituting (2) into this:
OC2=36+(64+8x)
OC2=100+8x
Step 7: Find x
Now we can relate OC to the triangle OAC:
Using the Pythagorean theorem again in triangle OAC:
OA2+AC2=OC2
Substituting the known values:
62+(8+x)2=OC2
36+(64+16x+x2)=OC2
100+16x+x2=OC2
Step 8: Equate and Solve
Now we equate the two expressions for OC^2:
100+8x=100+16x+x2
Simplifying gives:
0=8x+x2
Factoring out x:
x(x+8)=0
Thus, x=0 or x=−8 (not possible since lengths cannot be negative).
Step 9: Substitute Back to Find y
Substituting x=0 back into equation (2):
y2=64+8(0)=64
Thus, y=√64=8 cm.
Final Answer
The length of BC is:
8 cm
We have a circle with center O, diameter AB, and a tangent CB at point B. The line AC intersects the circle at point G. We know the radius of the circle (r) is 6 cm, and the length AG is 8 cm.
Since the radius is 6 cm, the diameter AB can be calculated as:
AB=2×r=2×6=12 cm
Using the property that the radius is perpendicular to the tangent at the point of tangency (point B), we can form a right triangle OBC, where:
- OB = radius = 6 cm
- BC = length we want to find (let's denote it as y)
- OC = length from the center O to point C
In triangle OBC, we can apply the Pythagorean theorem:
OB2+BC2=OC2
Substituting the known values:
62+y2=OC2
36+y2=OC2(1)
Next, we need to find OC. Since AG = 8 cm and G lies on the circle, we can express OC in terms of AG and CG. Let CG be x, then:
AC=AG+GC=8+x
Using the power of a point theorem, we have:
CB2=AG⋅AC
Substituting the known values:
y2=8⋅(8+x)
y2=64+8x(2)
Now we have two equations:
1. 36+y2=OC2
2. y2=64+8x
OC2=36+y2
Substituting (2) into this:
OC2=36+(64+8x)
OC2=100+8x
Now we can relate OC to the triangle OAC:
Using the Pythagorean theorem again in triangle OAC:
OA2+AC2=OC2
Substituting the known values:
62+(8+x)2=OC2
36+(64+16x+x2)=OC2
100+16x+x2=OC2
Now we equate the two expressions for OC^2:
100+8x=100+16x+x2
Simplifying gives:
0=8x+x2
Factoring out x:
x(x+8)=0
Thus, x=0 or x=−8 (not possible since lengths cannot be negative).
Substituting x=0 back into equation (2):
y2=64+8(0)=64
Thus, y=√64=8 cm.
The length of BC is:
8 cm
Topper's Solved these Questions
Similar Questions
In a circle centred at O, AB is a chord and C is any point on AB such that OC is perpendicular to AB. If the radius of the circle is 10 cm and OC = 6 cm, then the length of the chord is:
एक वृत्त में O केंद्र है , AB एक जीवा है और C, AB पर कोई बिंदु है जैसे OC, AB पर लंबवत है। यदि वृत्त की त्रिज्या 10 सेमी और OC = 6 सेमी है, तो जीवा की लंबाई ज्ञात करे |
View SolutionAB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?
View Solution
Knowledge Check
O is the centre of a circle. AB is a chord of the circle but not its diameter. OC is perpendicular to AB. If OC = CB and radius of the circle be 7 cm, then the length of AB is
A7√2cmB14cmC7 cmD7√2 cm
In the given figure, MP is the tangent to a circle with centre A and NQ is a tangent to a circle with centre B. If MP = 15 cm, NQ = 8 cm, PA = 17 cm and BQ = 10 cm, then AB is:
दी गयी आकृति में, MP एक वृत्त की स्पर्श रेखा है जिसका केंद्र A है तथा NQ उस वृत्त की स्पर्श रेखा है जिसका केंद्र B है | यदि MP = 15 सेमी, NQ = 8 सेमी, PA =17 सेमी तथा BQ = 10 सेमी है, तो AB का मान क्या होगा ?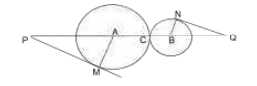
View SolutionThe vertices of △PQR lie on a circle with centre O. SR is a tangent to the circle at the point R. If QR bisects the ∠ORS, then what is the measure of ∠RPQ ?
त्रिभुज PQR के शीर्ष बिंदु एक वृत्त पर अवस्थित हैं जिसका केंद्र O है| SR बिंदु R पर वृत्त की स्पर्श रेखा है | यदि QR, ∠ORS को द्विभाजित करता है, तो कोण RPQ का माप ज्ञात करें |
View SolutionFrom a point P , outside a circle, PAB is a secant and PT is a tangent to the circle, where A , B and T are points on the circle. If PT = 5cm , PA = 4cm and AB = x , then x is equal to:
वृत्त के बाहर एक बिंदु P से , PAB एक छेदक रेखा तथा PT वृत्त की एक स्पर्श रेखा है एवं A, B और T वृत्त पर स्थित बिंदु हैं | यदि PT=5 सेमी, PA = 4 सेमी तथा AB = x सेमी है, तो x का मान किसके बराबर होगा ?
View SolutionTwo chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?
View SolutionFrom an external point P, a tangent PQ is drawn to a circle, with centre O, touching the circle at Q. If the distance of P from the centre is 13 cm and the length of the tangent PQ is 12 cm, then the radius of the circle is:
एक बाहरी बिंदु P से, केंद्र O वाले एक वृत्त पर एक स्पर्श रेखा PQ खींची जाती है, जो वृत्त को Q पर स्पर्श करती है | यदि केंद्र से P की दूरी 13 सेमी है तथा स्पर्श रेखा PQ की लंबाई 12 सेमी है, तो वृत्त की त्रिज्या कितनी होगी ?
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If ∠APB=40∘, then ∠OAB is equal to:
PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=40∘ है, तो ∠OAB का मान ज्ञात करें |
View Solution
