Question

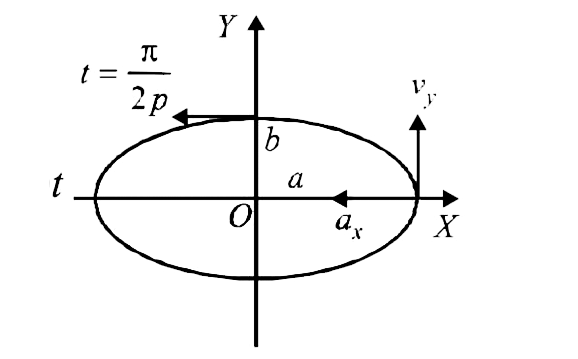
The coordinate of a particle moving in a plane are given by $x\left(t\right)=a\cos \left(pt\right)\text{and}y\left(t\right)=b\sin \left(pt\right)$ where $a,b(<a)$ and $P$ are positive constants of appropriate dimensions . Then

Options

A. the path of the particle is an ellipse
B. the velocity and acceleration of the particle are normal to each other at `t = pi//(2p)`
C. the accelaration of the particle is always directed towards a focus
D. the distance travelled by the particle in time interval ` t= 0 to t = pi//(2p)` is `a`

Answer

A::B::C

Explanation

` x = a cos pt rArr cos (pt) = x//a ` …(1)
` y = b sin pt rArr sin (pt) = y/b ` …(2)
Squaring and adding `(1) and (2)`, we get ,
` (x^(2))/(a^(2)) + (y^(2))/(b^(2)) = 1`
`:.` The path of the particle is an ellipse.
From the given equations we can find ,
` (dx)/(dt) = v_(x) = -ap sin pt , (dx )/(dt^(2)) = a_(x) = -ap^(2) cos pt `
` (dy)/(dt) = v_(y) = pb cos pt `
and `(d^(2)y)/dt^(2) = a_(y) = - bp^(2) sin pt `
At time `t = (pi)/(2p)` , or pt = (pi)/(2)`
`a_(x)` and `v_(y)` becomes zero (because `cos (pi)/(2) = 0)`.Only `v_(x)` and `a_(y)` are left ,
or we can say that velocity is along negative ` x-axis ` and acceleration along negative `y - axis` . Hence , at `t = (pi)/( 2p)` , velocity and acceleration of the particle are normal to each other.
At ` t = t` , position of the particle `vec r(t) = xhati + yhatj = xhati + yhatj = a cos p thati + b sin pthatj` and acceleration of the particle is
` a(t) = a_(x) hati + a_(y) hat j = - p^(2) [ a cos pt hat i + b sin pt hatj]`
` = - p^(2)[ xhati + yhatj ] = -p^(2) vec r(t)` Therefore , acceleration of the particle is always directed towards origin . At ` t= 0 `, particle is at `(a, 0)` and at `t = (pi)/(2p)`, particle is at `( 0, b)`. Therefore , the distance covered is one fourth of the elliptical path and not `a` .