A stone is thrown upwards and it rises to a height 0f 200m. The relative velocity of the stone with respect to the earth will be maximum at :-
Height of 100m
Height of 150m
Heighest point
The ground
The correct Answer is:D
To solve the problem, we need to analyze the motion of the stone thrown upwards and determine when its relative velocity with respect to the Earth is maximum.
1. Understanding the Motion:
- When a stone is thrown upwards, it moves against the force of gravity. Initially, it has a certain velocity (let's denote it as v0) when thrown.
2. Maximum Height:
- The stone will rise to a maximum height of 200 meters. At this point, the stone's velocity becomes zero momentarily before it starts falling back down.
3. Velocity During Ascent:
- As the stone ascends, its velocity decreases due to the acceleration due to gravity acting downwards. The stone's velocity at any point during its ascent can be expressed as:
v=v0−gt
where g is the acceleration due to gravity (approximately 9.81m/s2) and t is the time since it was thrown.
4. Relative Velocity:
- The relative velocity of the stone with respect to the Earth is the velocity of the stone minus the velocity of the Earth (which is stationary). Therefore, the relative velocity vrel is simply the velocity of the stone itself since the Earth’s velocity is zero:
vrel=v
5. When is Relative Velocity Maximum?:
- The relative velocity of the stone with respect to the Earth is maximum when the stone is at the point of release (the ground) because this is when the stone has its maximum initial velocity v0. As the stone rises, its velocity decreases until it reaches zero at the maximum height.
6. Conclusion:
- Therefore, the relative velocity of the stone with respect to the Earth will be maximum at the time of release, which is at the ground level.
Final Answer:
The relative velocity of the stone with respect to the Earth will be maximum at the ground level (when it is thrown).
- When a stone is thrown upwards, it moves against the force of gravity. Initially, it has a certain velocity (let's denote it as v0) when thrown.
- The stone will rise to a maximum height of 200 meters. At this point, the stone's velocity becomes zero momentarily before it starts falling back down.
- As the stone ascends, its velocity decreases due to the acceleration due to gravity acting downwards. The stone's velocity at any point during its ascent can be expressed as:
v=v0−gt
where g is the acceleration due to gravity (approximately 9.81m/s2) and t is the time since it was thrown.
- The relative velocity of the stone with respect to the Earth is the velocity of the stone minus the velocity of the Earth (which is stationary). Therefore, the relative velocity vrel is simply the velocity of the stone itself since the Earth’s velocity is zero:
vrel=v
- The relative velocity of the stone with respect to the Earth is maximum when the stone is at the point of release (the ground) because this is when the stone has its maximum initial velocity v0. As the stone rises, its velocity decreases until it reaches zero at the maximum height.
- Therefore, the relative velocity of the stone with respect to the Earth will be maximum at the time of release, which is at the ground level.
The relative velocity of the stone with respect to the Earth will be maximum at the ground level (when it is thrown).
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-341videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE28videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-199videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
Knowledge Check
- Question 1 - Select One
If an object is thrown upwards and rises to á height of 10 m. Calculate the velocity with which the object was thrown upwards and time taken by the object to reach the highest point.
A12m/s ,1 .43 sB14 m/s . 1.84 sC14 m/s , 1.43 sD12 m/s , 1.84 s - Question 2 - Select One
A body is thrown vertically upwards and rises to a height of 10m. The velocity with which the body was thrown is (g - 9.8m/(s2)
A10m/sB20m/sC14m/sDnone of these - Question 3 - Select One or More
Two stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u1=30m/sec and u2=50m/sec. Which of the curve represent correct variation (for the time interval in which both reach the ground) of
(x2−x1) = the relative position of second stone with respect to first with time (t)
(v2−v1) = the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.A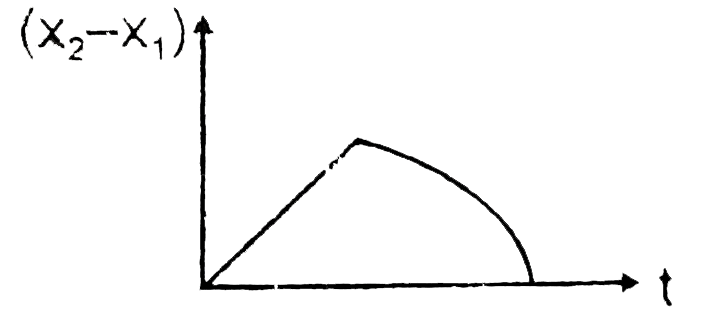 B
B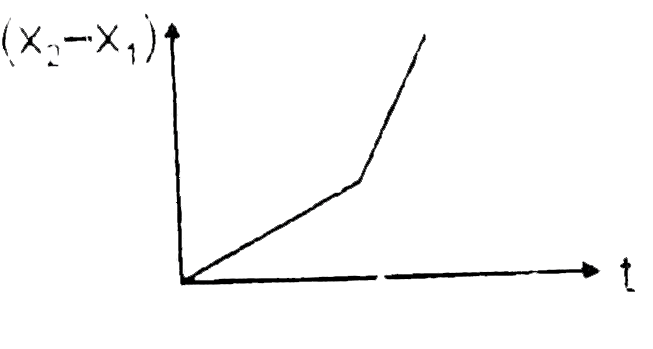 C
C D
D
From the top of a tower, a stone A is thrown upwards and a stone B is thrown downwards with the same speed. The velocity of stone A, on colliding with the ground is :
View SolutionA stone thrown upwards with speed u attains maximum height h. Ahother stone thrown upwards from the same point with speed 2u attains maximum height H. What is the relation between h and H?
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10ms−1 , then the maximum height attained by the stone is (g=10ms−2)
View SolutionA stone of 200g is thrown vertically upward at a velocity of 60m/s. The kientic energy of the stone after 7s will be (g=10m/s2)
View SolutionA stone thrown upward with a speed u from the top of a tower reaches the ground with a velocity 4u. The height of the tower is
View Solution

