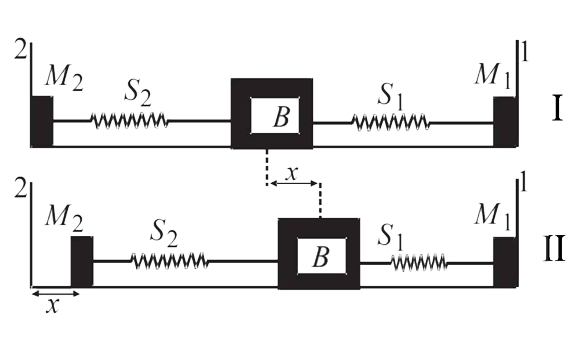
A block (B) is attached to two unstriched sprig S1 and S_(2) with spring constant K and 4K , respectively (see fig 1) The other ends are atteched in identical support M1 and M2 not attached in the walls . The springs and supports have negligible mass . There is no friction anywhere . The block B is displaced toword wall 1 by a small distance z (figure (ii)) and released . THe block return and moves a maximum displacements x and y are musured with reoact to the equalibrum of the block B and the ratio y/x is
4
2
1/2
1//4
The correct Answer is:C
( c) When the block B is displaced toward well 1 , only spring S1 is compressed and S2 is its natural same . This happens because this ofter end of S2 is not atteched to the will hat is free . Therefor the energy stored in the systen =12k1x2 when the block is will come back to the equlitbrum position and move toward well 2 As the happeens the spring S1 comes in its nature length and S2 gas compressed . As there are so frictional force invalved , the P E sound is the S1 gas street and at the PE of spring s1 when the block B its extreme posion after compressed s2 by y
∴12k1x2=12k2y2
12×kx2=124ky2,x2=4y2∴yx=12
Topper's Solved these Questions
Similar Questions
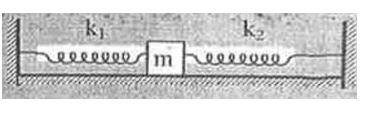
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
View Solution
Knowledge Check
A block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
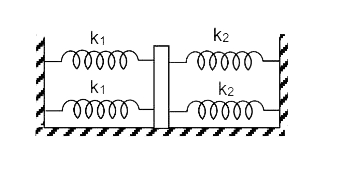 A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)mA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
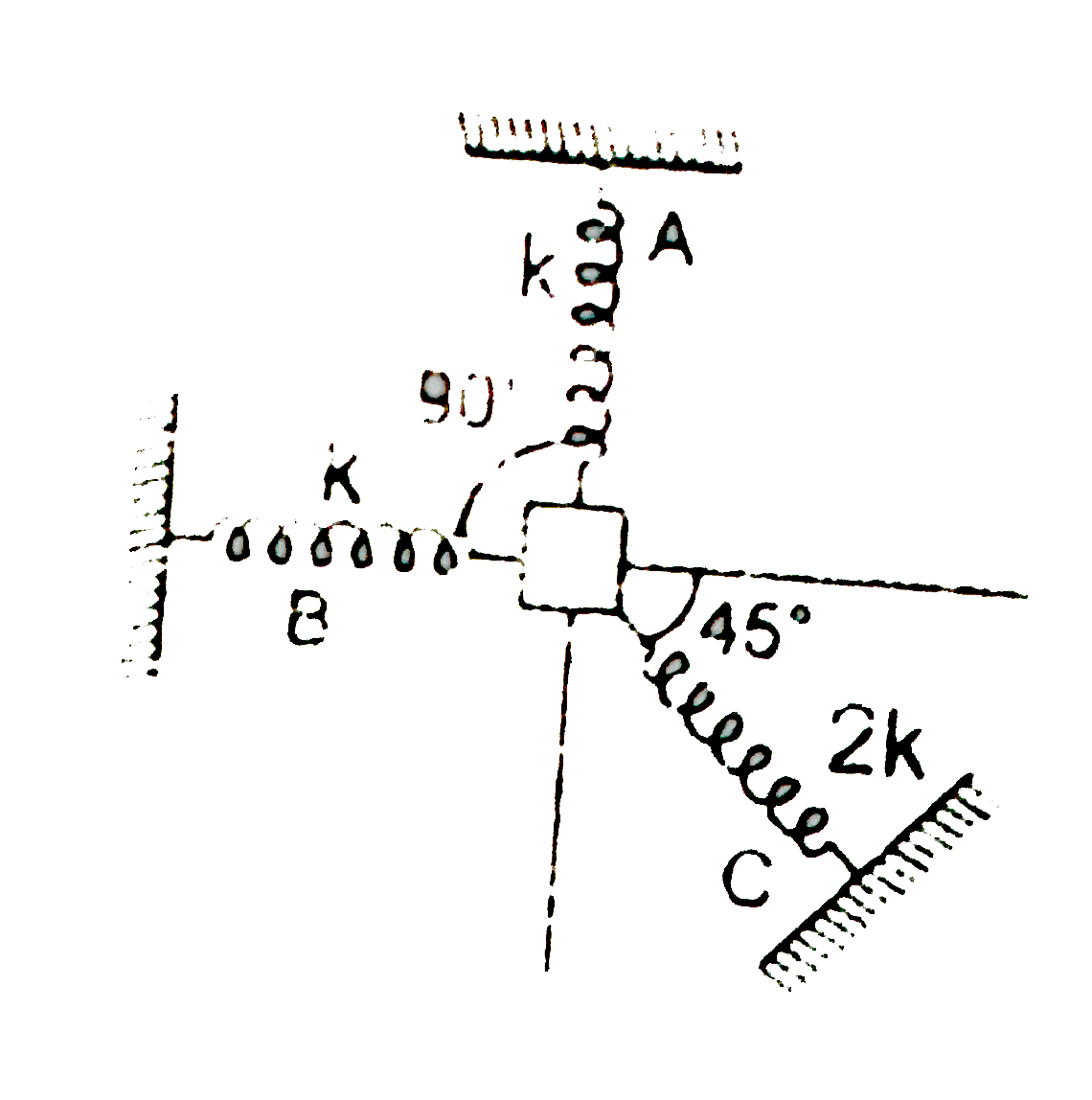
View SolutionTwo spring have force constants k1 and k2 respectively. They are attached to a mass m and two fixed supports as shwon in figure. If the surface is frictionless, fing the time period of oscillations. What is the spring factore of this combination.
View SolutionA block of mass M1 is attached with a spring constant k. The whole arrangement is placed on a vechile as shown in the figure. If the vehicle starts moving towards right with an acceleration a (there is no friction anywhere), then :
 .
.
View SolutionTwo masses m1 and m2 are attached to a spring balance S as shown in figure. m1>m2 then the reading of spring balance will be .
 .
.
View Solution