A block 'A' of mass 2m is placed on another block 'B' of mass 4m which in turn is placed on a fixed table. The two blocks have a same length 4d and they are placed as shown in fig The coefficient of friction (both static and kinetic) between the block 'B' and table is μ. There is no friction between the two blocks. A small object of mass m moving horizontally along a line passing through the centre of mass (cm.) of the block B and perpendicular to its face with a speed v collides elastically with the block B at a height d above the table.

(a) What is the minimum value of v(call it v0) required to make the block A topple?
(b) If v=2v0,find the distance (from the point P in the figure ) at which the mass m falls on the table after collision. (Ignore the role of friction during the collision).
The correct Answer is:A, B, C, D
Since the collision is elastic in nature applying conservation
of linear momentum and conservation of kinetic energy
mv=(4m)u+mv'
where u is the velocity of mass 4m after collision and v' is
the velocity of mass 2m
⇒v'=v−4u....(i)
Also, 12mv2=12(4m)u2+12mv'2
⇒v2=4u2+v2....(ii)
From (i) to (ii)
v2=4u2+(v−4u)2⇒u=2v5
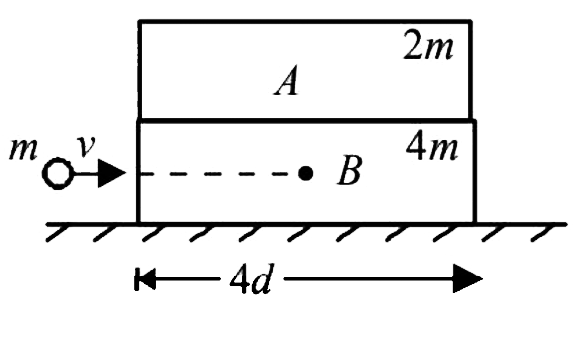
Block B starts moving but the block A remains at rest as
there is no friction between A and B
For block A to topple, block B should move a distance 2d.
Let the retardation produced in B due to friction force
between B and the table be a
F=μN⇒(4m)a=μ(6mg)⇒a=1.5μg
For the motion of B,
u=2v5,v=0,s=2d,a=−1.5μg
Now, v2−u2=2as⇒(0)2−(2v5)2=2(−1.5μg)2d
⇒v=52√6μgd
For elastic collision between two bodies
v1=(m1−m2)u1m1+m2+2m2u2m1+m2
Here, m1=m,m2=4m,u1=5√6μgd,u2=0
⇒v1=(m−4m)5√6μgdm+4m+0
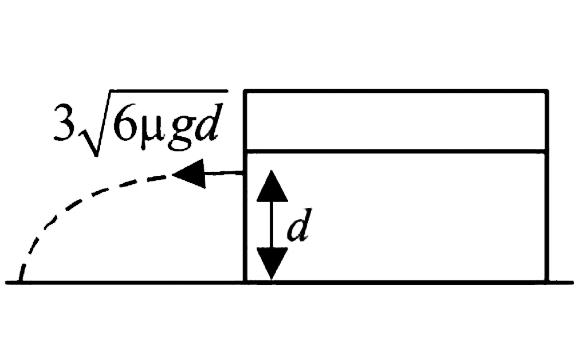
=−3×5√6μgd5=−3√6μgd
The negative sigh shows that the mass m rebounds.
It then follows a projectile motion.
Considering the vetical direction motion of this projectile.
uy=0,sy=d,ay=g,ty=?
s=ut+12at2⇒d=12>2⇒t=√2dg
The horizontal distance travelled by mass m during this
time t
x=3√6μgd×√2dg=6√3μd2=6d√3μ
Topper's Solved these Questions
Similar Questions
A block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
 .
.
View SolutionThe block of mass M and are arrenged as the situation in fig is shown.The coefficient of friction between two block is μand that between the bigger block and the ground is μ find the acceleration of the block
View Solution
Knowledge Check
A block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
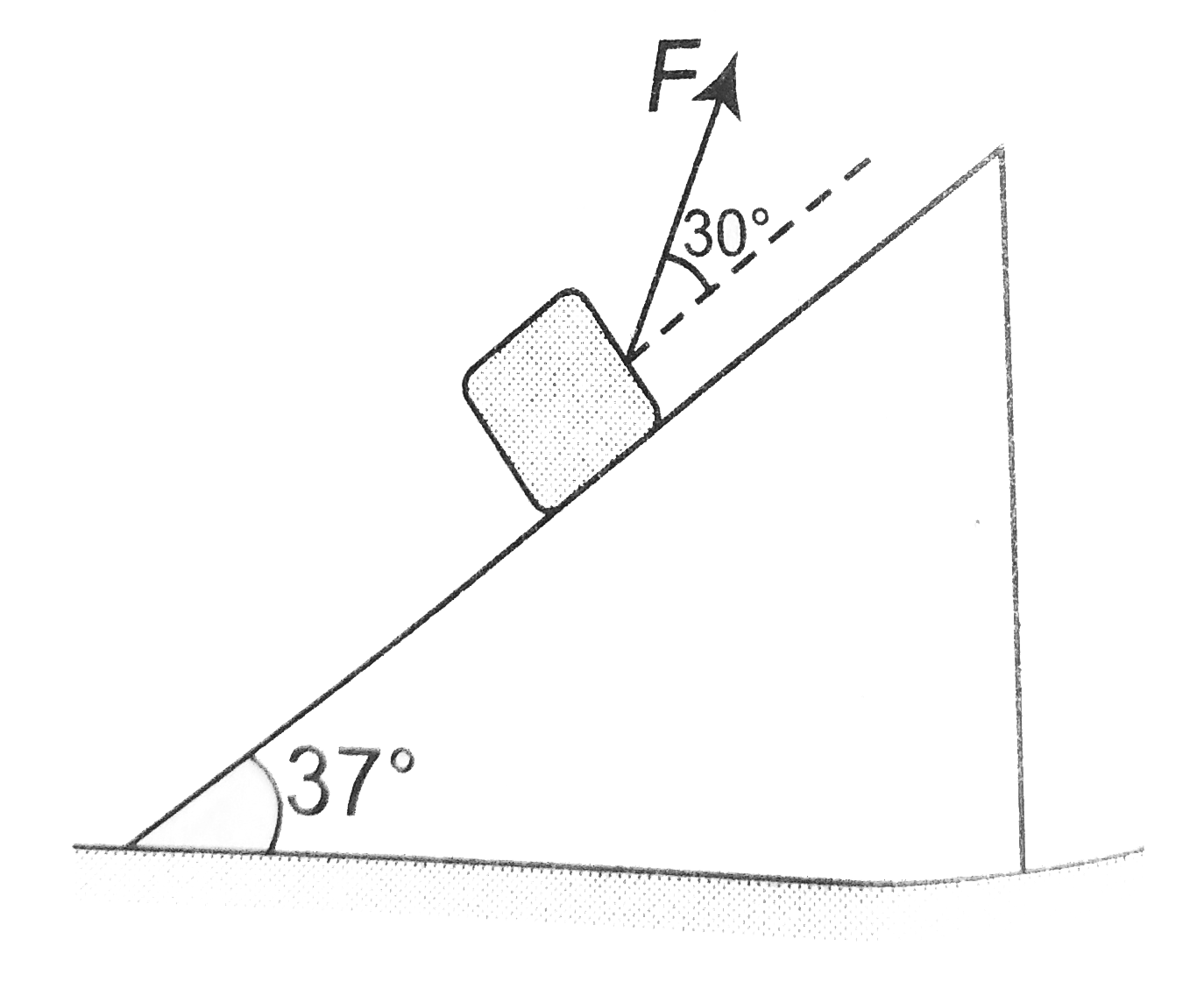 Astatic in nature in the direction up the plane and have the value 30.2NBstatic in nature in the direction down the plane and have the value 30.2NCkinetic in nature in the direction up the plane and have the value 30.2NDNone of these
Astatic in nature in the direction up the plane and have the value 30.2NBstatic in nature in the direction down the plane and have the value 30.2NCkinetic in nature in the direction up the plane and have the value 30.2NDNone of theseA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?
 A(M+m)(μ2−μ1)gB(M−m)(μ2−μ1)gC(M−m)(μ2+μ1)gD(M+m)(μ2+μ1)g
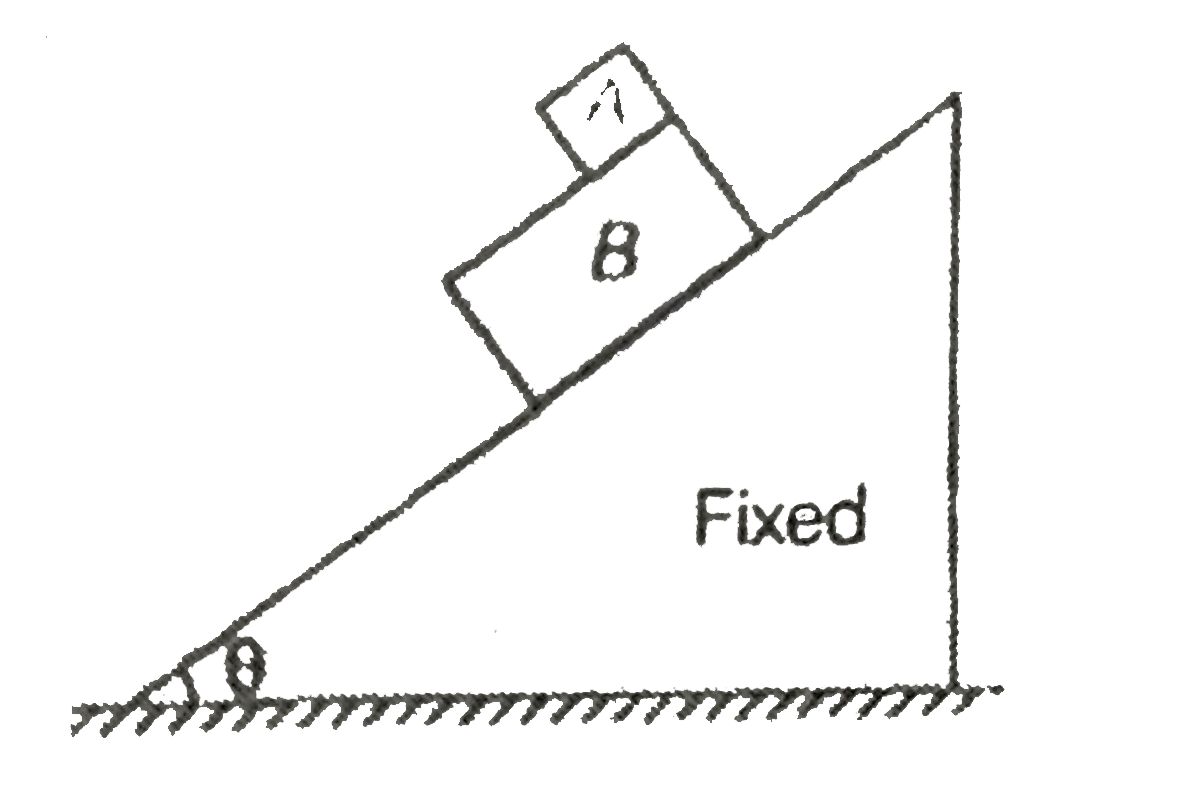
A(M+m)(μ2−μ1)gB(M−m)(μ2−μ1)gC(M−m)(μ2+μ1)gD(M+m)(μ2+μ1)gThe coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between A&B is released from rest & there is no slipping between A&B then:
 A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)
A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)
A block A slides over an another block B which is placed over a smooth inclined plane as shown in figure . The coefficient of friction between the two blocks A and B is μ . Mass of block B is two times the mass of block A . The acceleration of the centre of mass of two blocks is
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
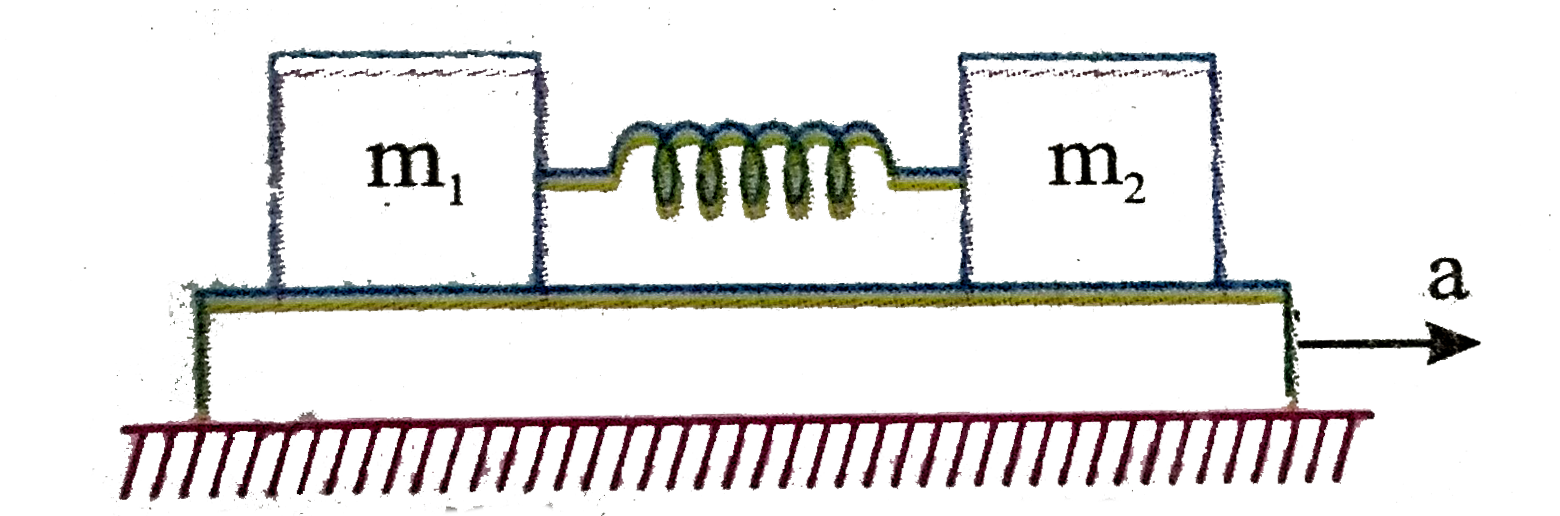
View Solution
