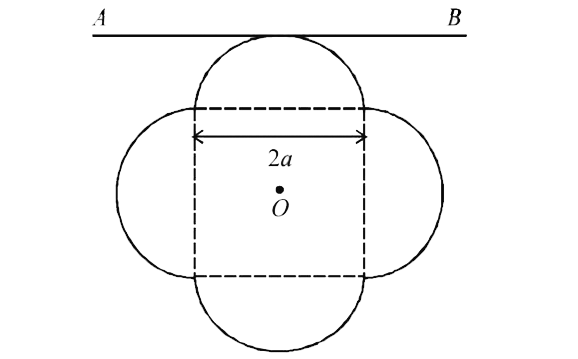
A symmetric lamina of mass M consists of a square shape with a semicircular section over of the edge of the square as shown in fig. p-10. The side of the square is 2a. The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is . The moment of inertia of the lamina is ......
The correct Answer is:A, B, D
Assuming symmetric lamina to in xy plane, we will have
(Since the mass distributon is same about x-axis and
y-axis
(perpendicular axis theorem)
it is given that
Hence
Now, according to parallel axis
theorem, we get
M

Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
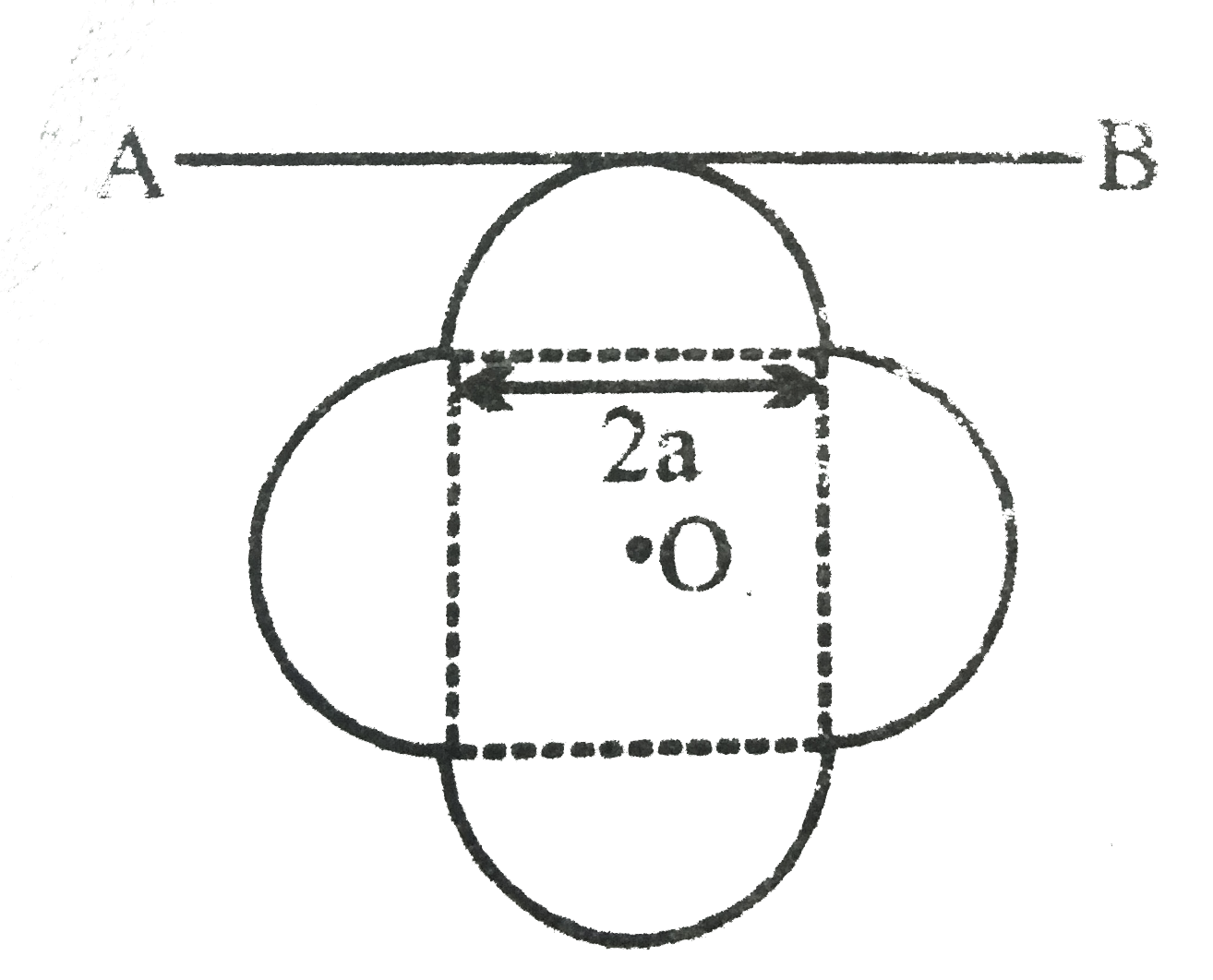
A symmetric lamina of mass M consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is 2a.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina about the tangent AB in the plane of lamina is.
 .
.
View SolutionThe moment of inertia of a disc about an axis through its centre and perpendicular to its plane is 12MR2 . Its moment of inertia about any diameter will be __________
View Solution
Knowledge Check
Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
AMR22−M(4R3π)2BMR22−M(√24R3π)2CMR22+M(4R3π)2DMR22+M(√24R3π)2Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2Four identical thin rods each of mass M and length l, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
A13Ml2B43Ml2C23Ml2D133Ml2
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
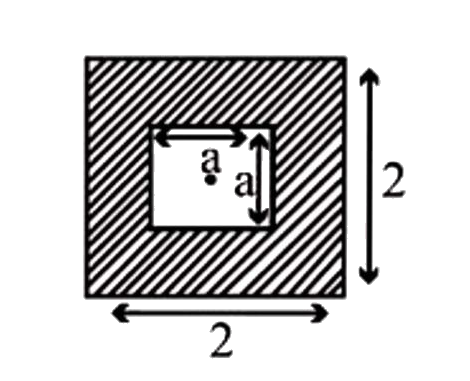
View SolutionIn the above problem, calculate the moment of inertia about an axis passing through point Q and perpendicular to the plane of square.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is I. What is the moment of inertia about its diameter ?
View Solution
