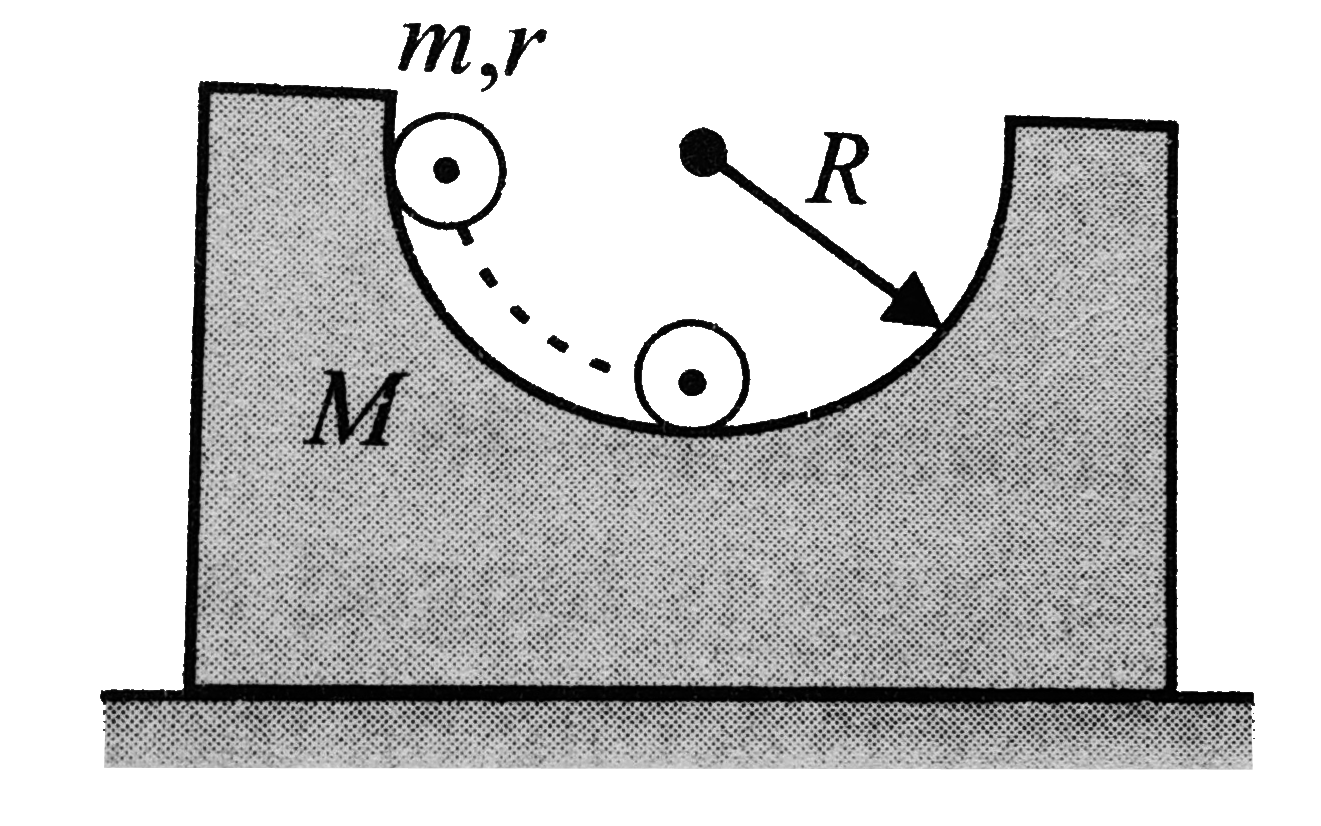
A block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?

The correct Answer is:B
C.M. of the system of two bodies in situation (i) in
x-coordinate
xC=M×0+mx1M+m = (mx_1)/(M+m) …..(i)<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_RM_C06_061_S01.pngwh=80%mx-autosty≤=background:white;><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_RM_C06_061_S02.pngwh=80%mx-autosty≤=background:white;><br>C.M.ofthesystem∈situation(ii)∈x−c∞rd∈ateis<br>x'_C = (Mxx x_2+mxx x_2)/(M+m) = x_2 ....(ii)<br>Sincenoexternalforceis∈x−direction<br>:. x_C = x'_C <br>:. x_2 = (mx_1 )/(M + m) = (m(R-r)/(M +m)<br>Apply∈gconservationofl∈earmomentum,<br>InitialMomentum=F∈alMomentum<br>0 = MV - mv<br>:. v = (MV)/(m) ......(iii)<br>Apply∈gtheconceptofconservationofe≠rgy,we≥t<br>Loss∈P.E.ofmassm=Ga∈∈K.E.ofmassMandGa∈∈<br>K.E.ofmassm<br>rArr mg(R - r) =(1)/(2)MV^2 + (1)/(2)mv^2<br>rArr 2mg (R-r) = MV^2 + m(M^2V^2)/(m^2)[om(iii)]
⇒2mg(R−r)=MV2+M2GV2m
2mg(R -r)=MV^2 [(1+(M)/(m)] = MV^2 [(m+M)/(m)]<br>rARr (2m^2g(R -r)/(M(m+M) = v^2 rArr V =m sqrt(2g(R -r )/(M(m+M))
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
A block of mass M with a semi circular track of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the top point A. The cylinder slips on the semicurcular frictionless track. How far has the block moved when the cylinder reaches the bottom of the track ? How fast is the block moving when the cylinder reaches the bottom of the track ?
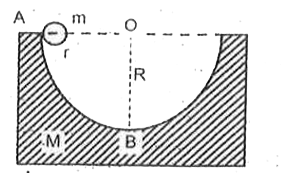
View SolutionA block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?
View Solution
Knowledge Check
A block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is (g=10ms−2)
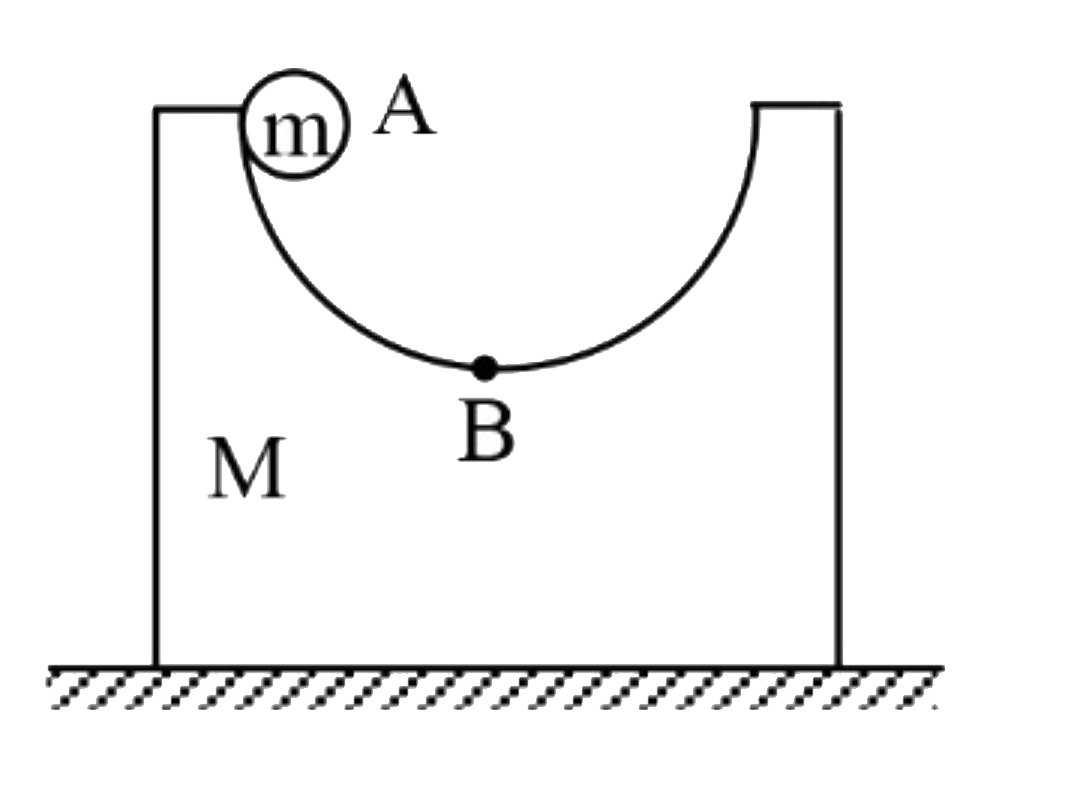 A√103ms−1B√43ms−1C√52ms−1D√10ms−1
A√103ms−1B√43ms−1C√52ms−1D√10ms−1A solid cylinder of radius 0.35 m is released from rest from a height of 1.8 m and rolls down the incline as shown in the figure. What is the angular speed of the cylinder when it reaches the horizontal surface?
 A8.2 rad/sB34 rad/sC14 rad/sD67 rad/s
A8.2 rad/sB34 rad/sC14 rad/sD67 rad/s
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k isA34MgsinθkB2MgsinθkCMgsinθkDnone of these
A block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionFigure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
View SolutionA uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is
View SolutionA block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
What is the magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom ?
View SolutionA mass M is supported by a massless string wound round a uniform cylinder ofmass M and radius R. On releasing the mass from rest, it will fall with acceleration?

View Solution
