Question

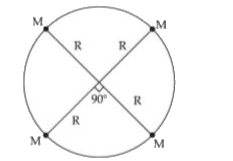
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:

Options

A. `sqrt((GM)/(R ))`
B. `sqrt(2sqrt2(GM)/(R ))`
C. sqrt((GM)/(R ) (1+2sqrt2))`
D. `(1)/(2)sqrt(GM)/(R ) (1+2sqrt2))`

Answer

D

Explanation

To find the speed of each particle moving in a circle under mutual gravitational attraction, we can follow these steps:

Step 1: Understand the Configuration
We have four particles, each of mass \( M \), positioned at the corners of a square with side length \( R \). The distance between any two adjacent particles is \( R \), and the distance between diagonal particles is \( \sqrt{2}R \).

Step 2: Calculate the Gravitational Force
Each particle experiences gravitational attraction from the other three particles. The gravitational force between any two particles is given by:
\( F = \frac{G M^2}{d^2} \)
where \( G \) is the gravitational constant and \( d \) is the distance between the particles.

Step 3: Identify Forces Acting on One Particle
For a particle (say particle A), the forces acting on it due to the other three particles (B, C, and D) need to be considered. The forces from B and C will act at an angle of 45 degrees to the line connecting A to the center of the square.

1. The force between A and B (distance \( R \)):
\( F_{AB} = \frac{G M^2}{R^2} \)

2. The force between A and C (distance \( R \)):
\( F_{AC} = \frac{G M^2}{R^2} \)

3. The force between A and D (distance \( \sqrt{2}R \)):
\( F_{AD} = \frac{G M^2}{( \sqrt{2}R )^2} = \frac{G M^2}{2R^2} \)

Step 4: Resolve Forces into Components
The forces \( F_{AB} \) and \( F_{AC} \) will have components along the radial direction (towards the center of the circle) and tangential direction. Since they are at 45 degrees:
- The radial components of \( F_{AB} \) and \( F_{AC} \) add up, while the tangential components will cancel out.

The total radial force \( F_r \) acting on particle A is:
\( F_r = F_{AB} \cos(45^\circ) + F_{AC} \cos(45^\circ) + F_{AD} \)
\( = \frac{G M^2}{R^2} \cdot \frac{1}{\sqrt{2}} + \frac{G M^2}{R^2} \cdot \frac{1}{\sqrt{2}} + \frac{G M^2}{2R^2} \)
\( = \sqrt{2} \cdot \frac{G M^2}{R^2} + \frac{G M^2}{2R^2} \)

Step 5: Set Up the Centripetal Force Equation
The centripetal force required to keep the particle moving in a circle of radius \( R \) is given by:
\( F_c = \frac{M v^2}{R} \)

Setting the total radial force equal to the centripetal force:
\( \sqrt{2} \cdot \frac{G M^2}{R^2} + \frac{G M^2}{2R^2} = \frac{M v^2}{R} \)

Step 6: Solve for Speed \( v \)
Rearranging gives:
\( v^2 = R \left( \sqrt{2} \cdot \frac{G M^2}{R^2} + \frac{G M^2}{2R^2} \right) \)
\( = \frac{G M^2}{R} \left( \sqrt{2} + \frac{1}{2} \right) \)
\( = \frac{G M^2}{R} \left( \frac{2\sqrt{2} + 1}{2} \right) \)

Taking the square root gives:
\( v = \sqrt{\frac{G M}{R} \cdot \frac{2\sqrt{2} + 1}{2}} \)

Final Answer
Thus, the speed of each particle is:
\( v = \sqrt{\frac{G M}{R} \cdot \frac{2\sqrt{2} + 1}{2}} \)

---