A glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,

(a) air from end 1 flows towards end 2. No change in the volume of the soap bubbles
(b) air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases
(c) no changes occurs
(d) air from end 2 flows towards end 1. volume of the soap bubble at end 1 increases
The correct Answer is:B
We know that excess pressure in a soap bubble is inversely proportinal to its radius. The soap bubble at end 1 has small radius as compared to the soap bubble at end 2(given). Therefore excess pressure at 1 is more.
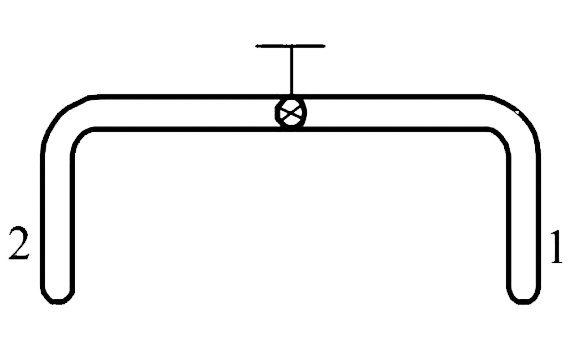
As the value is opened, air flows from end 1 to end 2 and the volume of soap bubble at end 1 decreases.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
- LAWS OF MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - LAWS OF MOTIONEXERCISE - JEE Main And Advanced
79 Videos
- MOMENTUM & IMPULSEBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOMENTUM & IMPULSEEXERCISE - JEE Main And Advanced
30 Videos
Similar Questions
Knowledge Check
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.
 Aair from end 1 flows towards 2. No change in the volume of the soap bubblesBair from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesCno change occursDair form end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.
Aair from end 1 flows towards 2. No change in the volume of the soap bubblesBair from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesCno change occursDair form end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.Two spherical soap bubbles of radii r1 and r2 in vacuume collapse under isothermal condition. The resulting bubble has radius R such that
AR=r1+r2BR=(r1+r2)12CR=√r21+r22DR=[(r2r2(r1+r2)]An isolated and charged spherical soap bubble has a radius 'r' and the pressure inside is atmospheric. If 'T' is the surface tension of soap solution, then charge on drop is:
A2√2rTε0B8πr√2rTε0C8πr√rTε0D8πr√2rTε0
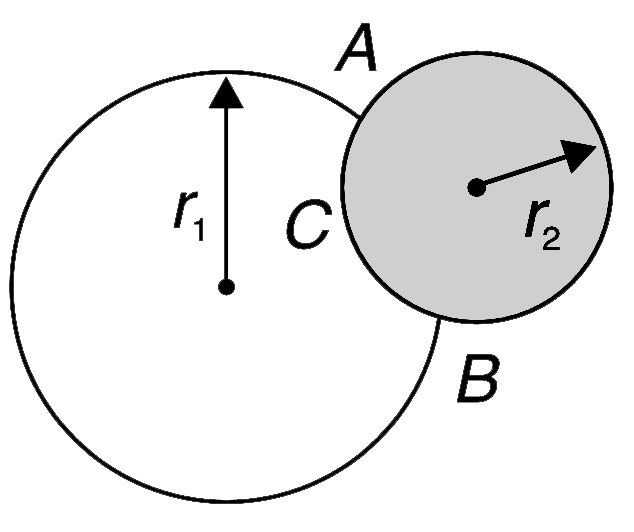
Two soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionTwo spherical soap bubbles of a radii 1 cm and 2 cm vacuum coalesce under isothermal conditions . The resultant bubble has a radius of
View SolutionA soap bubble A of radius 0.03 m and another bubble B of radius 0.04 m are brought together, so that the combined bubble has a common interface of radius r, then the value of r is
View SolutionTwo unequal soap bubbles are formed one on each side of a tube closed in the middle by a tap. What happens when the tap is opened to put the two bubbles in communication?
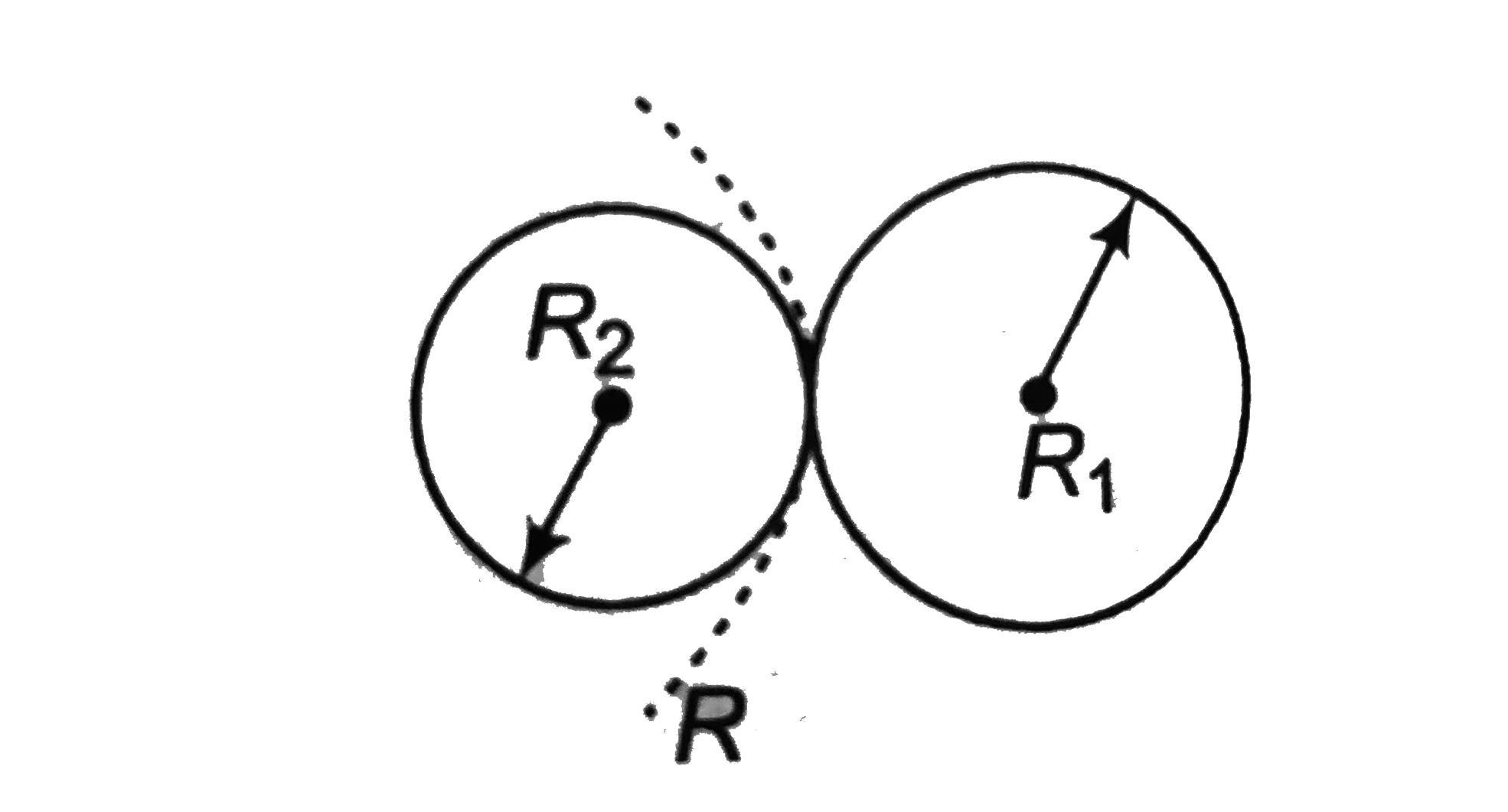
View SolutionTwo soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
 .
.
View Solution