A container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
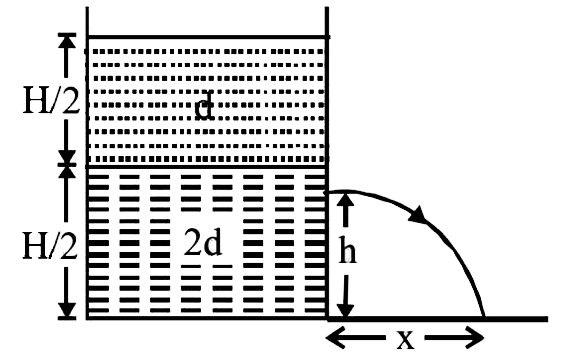
(a) A homogeneous solid cylinder of length L(L<H/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid. Determine:
(i) the density D of the solid and
(ii) the total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). Determine:
(i) the initial speed of efflux of the liquid at the hole,
(ii) the horizontal distance x travelled by the liquid initially, and
(iii) the height hm at which the hole should be punched so that the liquid travels the maximum distance xm initially. Also calculate xm.
The correct Answer is:A, B, C, D
(a) (i)
KEY CONCEPT:
Since the cylinder is in equilibrium in the liquid therefore
Weight of cylinder=upthrust
mg=FT1+FT2 where
FT1 and FT2 = upthrust due to lower and upper liquid respectively

A5×L×D×g=A5×L4×2d×g+A5×3L4×d×g
⇒D=2d4+3d4=5d4
(ii) Total pressure at the bottom of the cylinder=
Atmospheric pressure + Pressure due to liquid of density d+ Pressure due to liquid of density 2d+
Pressure due to cylinder [Weight/Area]
P=P0+H2dg+H2×2d×g+A5×L×D×gA
⇒P=P0+(3H2+L4)dg [∵D=5d4]
(b) KEY CONCEPT:
Applying Bernoulli's theorem
P0+[H2×d×g+(H2−h)2d×g]
=P0+12(2d)v2⇒v=√3H−4h2g
Horizontal Distance x
ux=v, t=t, x=vt ...(i)
For vertical motion of liquid falling from hole
uy=0, Sy=h, ay=g, ty=t
S=ut+12at2
⇒h=12>2⇒t=√2hg ...(ii)
<br>From(i)and(ii)<br>x=v_yxxsqrt((2h)/(g))=sqrt((3H-4h)g/2)xxsqrt((2h)/(g))<br>=sqrt((3H-4h)h)...(iii)<br>Forf∈d∈gthevalueofhforwhichxismaxiμm,wed⇔erentiateequation(iii)w.r.t.t<br>(dx)/(dt)=1/2[(3H-4h)h]^(-1//2){3H-8h}<br>Pu∈g(dx)/(dt)=0forf∈d∈gvalueshformaximaminima<br>1/2[(3H-4h)]^(-1//2)[3H-8h]=0impliesh=(3H)/(8)<br>:. x_m=sqrt([3H-4((3H)/(8))](3H)/(8))[From(iii)]<br>=sqrt((12H)/(8)xx(3H)/(8))=(6H)/(8)=(3H)/(8)

Topper's Solved these Questions
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
- LAWS OF MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - LAWS OF MOTIONEXERCISE - JEE Main And Advanced
79 Videos
- MOMENTUM & IMPULSEBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOMENTUM & IMPULSEEXERCISE - JEE Main And Advanced
30 Videos
Similar Questions
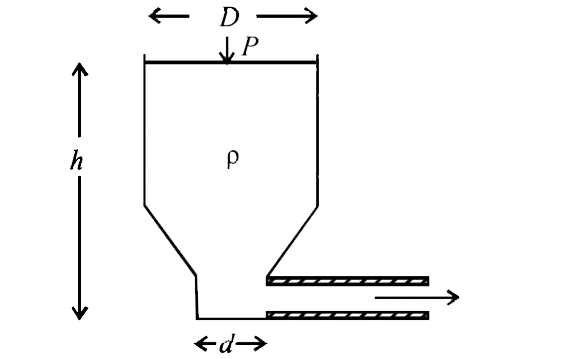
Shown in the figure is a container whose top and botoom diameters are D and d respectively. At the bottom of the container, there is a capillary tube of outer radius b and inner radius a.
The volume flow rate in the capillary is Q. If the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as ρ. Calculate the coefficient of viscosity η.
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA particle of mass 4 m which is at rest explodes into three fragments. Two of the fragments each of mass m are found to move with a speed v each in mutually perpendicular directions. The total energy released in the process of explosion is ............
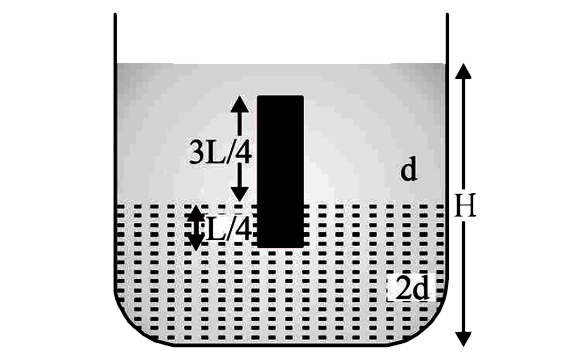
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P_0 . Then density D of solid is given by
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The density D of the material of the floation cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial value of x is
View SolutionA container of large uniform cross sectional area A resting on a horizontal surface holds two immiscible non-viscous and incompressible liquids of density d and 3d each of height H/2. The lower density liquid is open to the atmosphere having pressure P_o . A tiny hole of area a (a lt lt A) is punched on the vertical side of the lower container at a height h (0 lt h lt H/2) for which range is maximum.
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d , each of height H//2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L lt (H)/(2)) , cross-sectional area A//5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L//4 denser liquid. Determine (a) density D of the solid and (b) the total pressure at the bottom of the container. (Atmospheric pressure = P_0 ). .
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two-immiscible, non-viscous & incompressible liquids of densities d & 2d, each of height H/2. The lower density liquid is open to the atmoshpere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) corss-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid interface with the length L/4 in the denser liquid. Determine : (i) The density D of the solid & (ii) The total pressure at the bottom of the container.
View SolutionA vessel of large uniform cross-sectional area resting on a horizontal surface holds two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2. If a small hole is punched on the vertical side of the container at a heighth h(h<H2) the efflux speed of the liquid al the hole is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The density D of the material of the floating cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial speed of efflux without cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial value of x is
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P0. Then density D of solid is given by
View Solution
