A spring of force constant 800N/m has an extension of 5cm. The work done in extending it from 5cm to 15cm is
(a) 16J
(b) 8J
(c) 32J
(d) 24J
The correct Answer is:B
To find the work done in extending a spring from 5 cm to 15 cm, we can use Hooke's law and the formula for work done on a spring. Here’s a step-by-step solution:
Step 1: Understand the problem
We have a spring with a force constant (k) of 800 N/m, and we want to calculate the work done in extending it from an initial extension of 5 cm to a final extension of 15 cm.
Step 2: Convert units
Since the spring constant is given in N/m, we need to convert the extensions from centimeters to meters:
- Initial extension (x1) = 5 cm = 0.05 m
- Final extension (x2) = 15 cm = 0.15 m
Step 3: Use the work done formula
The work done (W) in stretching or compressing a spring is given by the formula:
W=12k(x22−x21)
Where:
- k is the spring constant,
- x1 is the initial extension,
- x2 is the final extension.
Step 4: Substitute the values into the formula
Substituting the values we have:
W=12×800N/m×((0.15)2−(0.05)2)
Step 5: Calculate the squares
Calculate (0.15)2 and (0.05)2:
(0.15)2=0.0225
(0.05)2=0.0025
Step 6: Find the difference
Now, find the difference:
0.0225−0.0025=0.02
Step 7: Substitute back into the work formula
Now substitute this difference back into the work formula:
W=12×800×0.02
Step 8: Calculate the work done
W=400×0.02=8J
Final Answer
The work done in extending the spring from 5 cm to 15 cm is 8 Joules.
---
We have a spring with a force constant (k) of 800 N/m, and we want to calculate the work done in extending it from an initial extension of 5 cm to a final extension of 15 cm.
Since the spring constant is given in N/m, we need to convert the extensions from centimeters to meters:
- Initial extension (x1) = 5 cm = 0.05 m
- Final extension (x2) = 15 cm = 0.15 m
The work done (W) in stretching or compressing a spring is given by the formula:
W=12k(x22−x21)
Where:
- k is the spring constant,
- x1 is the initial extension,
- x2 is the final extension.
Substituting the values we have:
W=12×800N/m×((0.15)2−(0.05)2)
Calculate (0.15)2 and (0.05)2:
(0.15)2=0.0225
(0.05)2=0.0025
Now, find the difference:
0.0225−0.0025=0.02
Now substitute this difference back into the work formula:
W=12×800×0.02
W=400×0.02=8J
The work done in extending the spring from 5 cm to 15 cm is 8 Joules.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
- LAWS OF MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - LAWS OF MOTIONEXERCISE - JEE Main And Advanced
79 Videos
- MOMENTUM & IMPULSEBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOMENTUM & IMPULSEEXERCISE - JEE Main And Advanced
30 Videos
Similar Questions
Knowledge Check
A spring of force constant 800N/m has an extension of 5cm. The work done in extending it from 5cm to 15cm is
A16 JB8 JC32 JD24 JA spring of force constant 800 N/m has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is:
A16 JB8 JC32 JD24 JA spring of force constant 800Nm−1has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is
A16JB8JC32JD24 J
A spring of force constant 800N/m has an extension of 5cm. The work done in extending it from 5cm to 15cm is
View SolutionA spring of force constant 800Nm−1 is stretched initially by 5cm. The work done in stretching from 5cm to 15cm is
View SolutionA spring with spring constant k is extended from x=0 to x=x1. The work done will be
View SolutionK is the force constant of a spring. The work done in increasing its extension from l1 to l2 will be
View SolutionTwo springs of force constant 100N/m and 150N/m are in series as shown the block is pulled by a distance of 2.5 cm to the right from equilibrium position what is the ratio of work done by the spring at left to the work done by the spring at right:
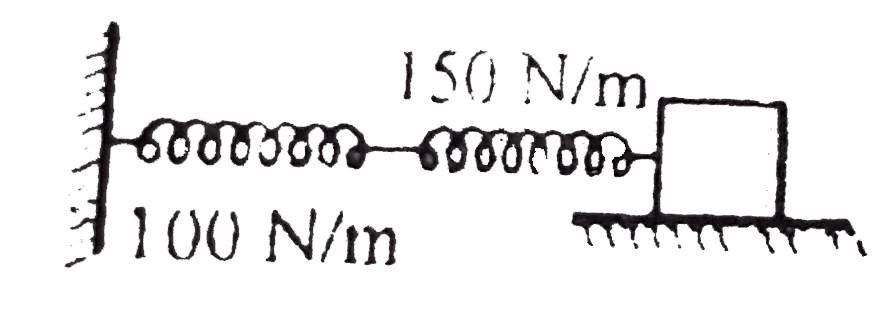
View Solution
