Water is flowing continuously from a tap having an internal diameter 8×10−3m. The water velocity as it leaves the tap is 0.4ms−1. The diameter of the water stream at a distance 2×10−1m below the tap is close to:
(a) 7.5×10−3m
(b) 9.6×10−3m
(c) 3.6×10−3m
(d) 5.0×10−3m
The correct Answer is:C
To find the diameter of the water stream at a distance of 2×10−1m below the tap, we can use the principle of conservation of mass, specifically the equation of continuity for incompressible fluids. The equation states that the product of the cross-sectional area and the velocity of the fluid must remain constant along the flow.
1. Identify Given Values:
- Internal diameter of the tap, d1=8×10−3m
- Velocity of water at the tap, v1=0.4m/s
- Distance below the tap, h=2×10−1m
2. Calculate the Cross-Sectional Area at the Tap:
The cross-sectional area A1 of the tap can be calculated using the formula for the area of a circle:
A1=π(d12)2=π(8×10−32)2
A1=π(4×10−3)2=π×16×10−6m2=16π×10−6m2
3. Apply the Equation of Continuity:
According to the equation of continuity:
A1v1=A2v2
where A2 is the cross-sectional area of the stream at a distance h below the tap, and v2 is the velocity at that point.
4. Assuming the Velocity at h is the Same:
For simplicity, we can assume that the velocity of the water stream remains approximately the same at h (since the height is not very large compared to the diameter). Thus, v2≈v1=0.4m/s.
5. Calculate the Cross-Sectional Area at h:
Rearranging the equation of continuity gives:
A2=A1v1v2=A1
Therefore, A2 remains the same as A1 under our assumption.
6. Calculate the Diameter at h:
Since A2 is the same, we can find the diameter d2 using:
A2=π(d22)2
Setting A2=A1:
16π×10−6=π(d22)2
Dividing both sides by π:
16×10−6=(d22)2
Taking the square root:
d22=4×10−3⟹d2=8×10−3m
7. Conclusion:
The diameter of the water stream at a distance 2×10−1m below the tap is approximately 8×10−3m.
- Internal diameter of the tap, d1=8×10−3m
- Velocity of water at the tap, v1=0.4m/s
- Distance below the tap, h=2×10−1m
The cross-sectional area A1 of the tap can be calculated using the formula for the area of a circle:
A1=π(d12)2=π(8×10−32)2
A1=π(4×10−3)2=π×16×10−6m2=16π×10−6m2
According to the equation of continuity:
A1v1=A2v2
where A2 is the cross-sectional area of the stream at a distance h below the tap, and v2 is the velocity at that point.
For simplicity, we can assume that the velocity of the water stream remains approximately the same at h (since the height is not very large compared to the diameter). Thus, v2≈v1=0.4m/s.
Rearranging the equation of continuity gives:
A2=A1v1v2=A1
Therefore, A2 remains the same as A1 under our assumption.
Since A2 is the same, we can find the diameter d2 using:
A2=π(d22)2
Setting A2=A1:
16π×10−6=π(d22)2
Dividing both sides by π:
16×10−6=(d22)2
Taking the square root:
d22=4×10−3⟹d2=8×10−3m
The diameter of the water stream at a distance 2×10−1m below the tap is approximately 8×10−3m.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
- LAWS OF MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - LAWS OF MOTIONEXERCISE - JEE Main And Advanced
79 Videos
- MOMENTUM & IMPULSEBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOMENTUM & IMPULSEEXERCISE - JEE Main And Advanced
30 Videos
Similar Questions
A shower head having 20 holes each of 0.1 cm in diameter is connected to a water pipe having an internal diameter of 1.8 cm. The speed of water flowing in the pipe is 108 cms−1. Calculate the speed of water leaving the shower head holes.
View SolutionWater is flowing at a speed of 0.5 m/s through a horizontal pipe of internal diameter 3 cm. Determine the diameter of the nozzle if the water is to emerge at a speed of 3 m/s.
View Solution
Knowledge Check
Water is flowing continuously from a tap having an internal diameter 8×10−3m. The water velocity as it leves the tap is 0.4ms−1. The diameter of the water stream at a distance 2×10−1m below the tap is close to (g=10m/s2)
A7.5×10−3mB9.6×10−3mC3.6×10−3mD5.0×10−3mWater is flowing continuously from a tap having an internal diameter 8×10−3 m. The water velocity as it leaves the tap is 0.4 m/s. The diameter of the water stream at a distance 2×10−1 m below the tap is close to
A7.5×10−3mB9.6×10−3mC3.6×10−3mD5.0×10−3mWater is flowing continuously from a tap having an internal dimeter 8×10−3m . The water then, water rises up in it leaves the tap is 0.4ms−1 . The diameter of the water stream at a distance 2×10−1m beblow the tap is close to
A7.5×10−3mB9.6×10−3mC3.6×10−3mD5.0×10−3m
Water is flowing condinuously from a tap of area 10−4m2 the water velocity as it leaves the top is 1m/s find out area of the water stream at a distance 0.15 m below the top
View SolutionWater is flowing in a pipe of diameter 4 cm with a velocity 3m/s . The water then enters into a tube of diameter 2 cm . The velocity of water in the other pipe is
View SolutionThe figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)
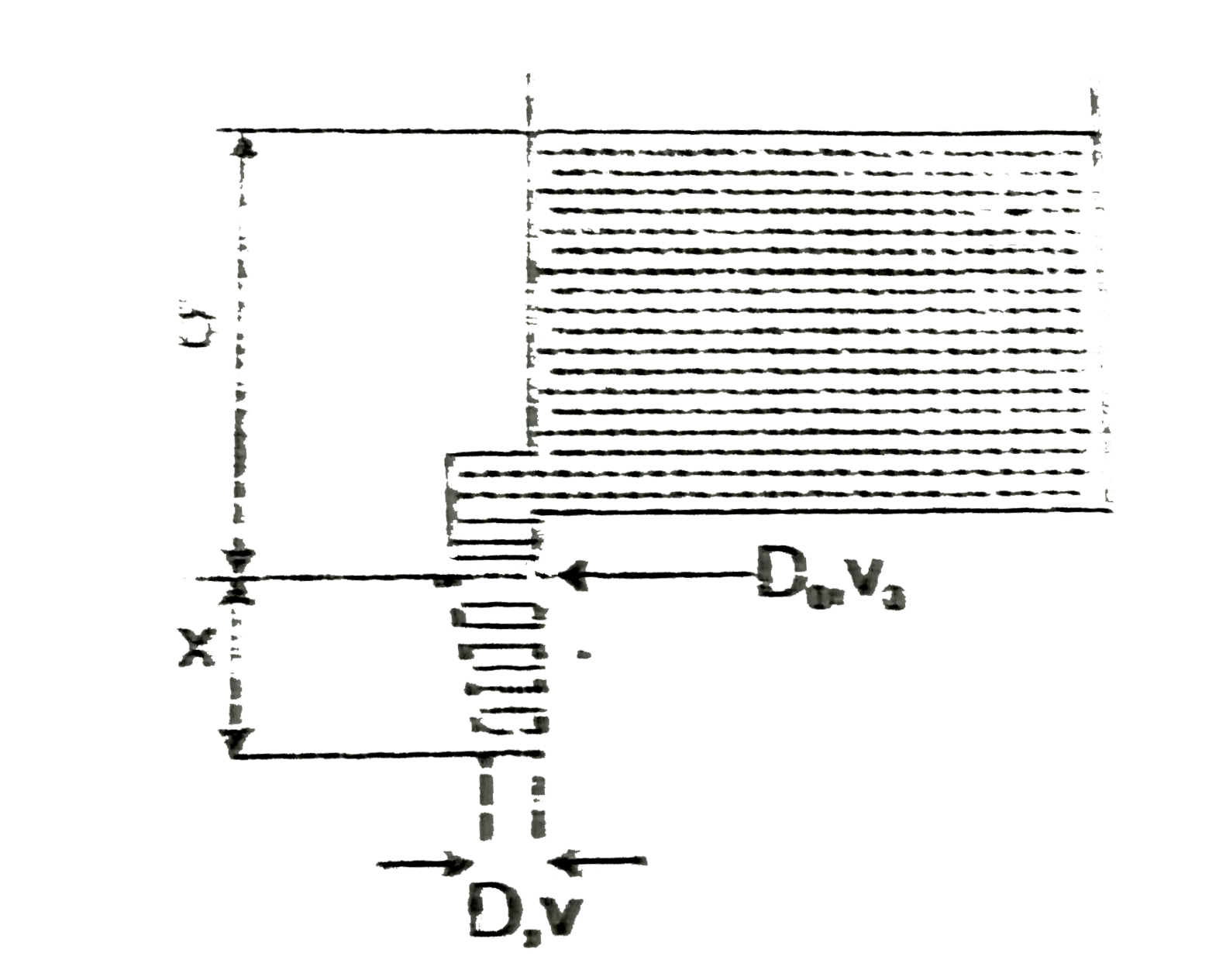
A student observes after setting up this experiment that for a tap with D0=1cm at x=0.3m the stream diameter D=0.9cm. The heights b of the water above the tap in this case will be:
View SolutionThe figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)
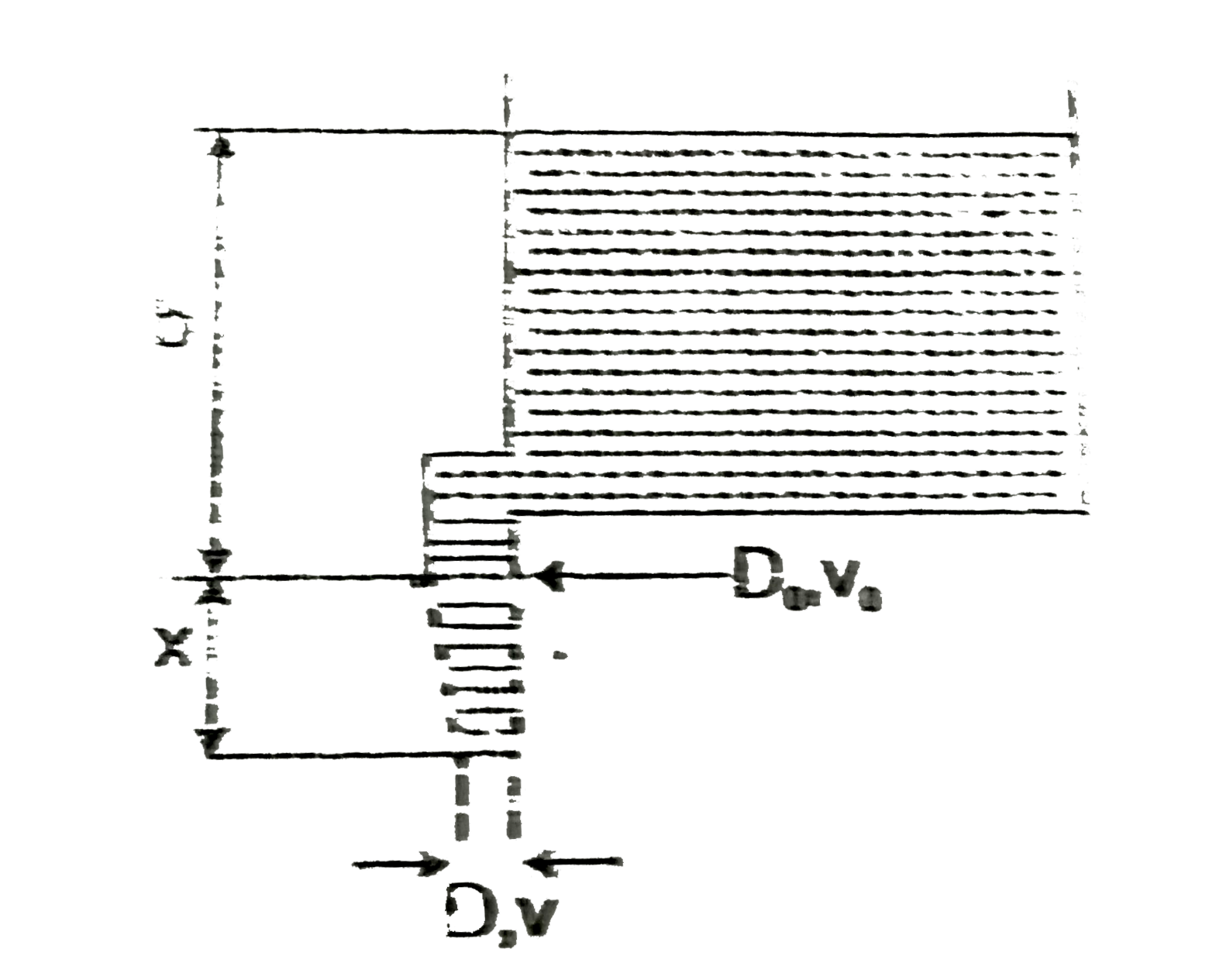
The equation for the water speed v as a funcation of the distance x below the tap will be:
View SolutionThe figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)

Equation for the stream diameter D in terms of x and D0 will be :
View Solution
