An open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)
(a) 16cm
(b) 22cm
(c) 38cm
(d) 6cm
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Initial Conditions
We have an open glass tube immersed in mercury, with a length of 8 cm extending above the mercury level. The tube is then closed and sealed.
Step 2: Raise the Tube
The tube is raised vertically by an additional 46 cm. Therefore, the total length of the tube that is now above the mercury level is:
Total height above mercury=8cm+46cm=54cm
Step 3: Define Variables
Let x be the height of the mercury column that rises in the tube when it is raised. The new height of the air column above the mercury will then be:
Height of air column=54cm−x
Step 4: Apply Pressure Conditions
The pressure at the top of the air column inside the tube is equal to the atmospheric pressure minus the height of the mercury column:
P=P0−x
Where P0=76cm of Hg.
Step 5: Use the Ideal Gas Law
Using the ideal gas law, we can write:
P1V1=P2V2
Where:
- P1=76cm (initial pressure)
- V1=8cm (initial volume)
- P2=76−xcm (final pressure)
- V2=54−xcm (final volume)
Step 6: Set Up the Equation
Substituting the known values into the equation gives:
76×8=(76−x)(54−x)
Step 7: Expand and Rearrange
Expanding the right side:
608=(76×54)−(76x+54x−x2)
Calculating 76×54:
76×54=4104
So, we have:
608=4104−(130x−x2)
Rearranging gives:
x2−130x+(4104−608)=0
This simplifies to:
x2−130x+3496=0
Step 8: Solve the Quadratic Equation
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=−130,c=3496:
x=130±√(−130)2−4⋅1⋅34962⋅1
Calculating the discriminant:
(−130)2−4⋅1⋅3496=16900−13984=2916
Thus,
x=130±√29162
Calculating √2916=54:
x=130±542
This gives two possible solutions:
1. x=1842=92cm
2. x=762=38cm
Step 9: Determine the Length of the Air Column
Using x=38cm:
Length of air column=54−x=54−38=16cm
Final Answer
The length of the air column above the mercury in the tube after raising it is:
16cm
We have an open glass tube immersed in mercury, with a length of 8 cm extending above the mercury level. The tube is then closed and sealed.
The tube is raised vertically by an additional 46 cm. Therefore, the total length of the tube that is now above the mercury level is:
Total height above mercury=8cm+46cm=54cm
Let x be the height of the mercury column that rises in the tube when it is raised. The new height of the air column above the mercury will then be:
Height of air column=54cm−x
The pressure at the top of the air column inside the tube is equal to the atmospheric pressure minus the height of the mercury column:
P=P0−x
Where P0=76cm of Hg.
Using the ideal gas law, we can write:
P1V1=P2V2
Where:
- P1=76cm (initial pressure)
- V1=8cm (initial volume)
- P2=76−xcm (final pressure)
- V2=54−xcm (final volume)
Substituting the known values into the equation gives:
76×8=(76−x)(54−x)
Expanding the right side:
608=(76×54)−(76x+54x−x2)
Calculating 76×54:
76×54=4104
So, we have:
608=4104−(130x−x2)
Rearranging gives:
x2−130x+(4104−608)=0
This simplifies to:
x2−130x+3496=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=−130,c=3496:
x=130±√(−130)2−4⋅1⋅34962⋅1
Calculating the discriminant:
(−130)2−4⋅1⋅3496=16900−13984=2916
Thus,
x=130±√29162
Calculating √2916=54:
x=130±542
This gives two possible solutions:
1. x=1842=92cm
2. x=762=38cm
Using x=38cm:
Length of air column=54−x=54−38=16cm
The length of the air column above the mercury in the tube after raising it is:
16cm
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
- LAWS OF MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - LAWS OF MOTIONEXERCISE - JEE Main And Advanced
79 Videos
- MOMENTUM & IMPULSEBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOMENTUM & IMPULSEEXERCISE - JEE Main And Advanced
30 Videos
Similar Questions
An open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)
View Solution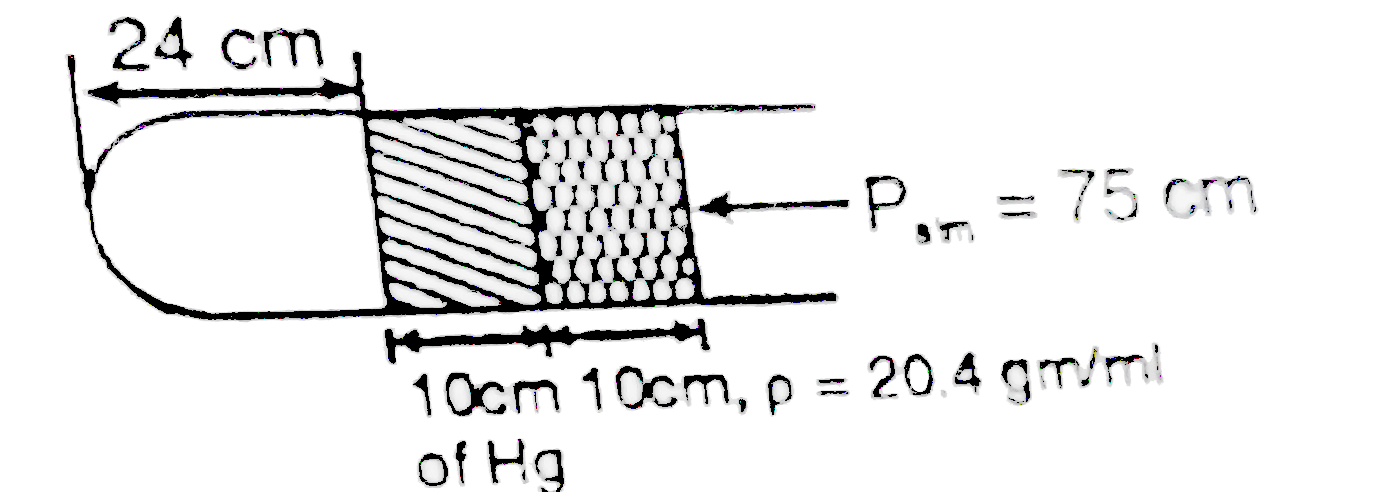
If above tube is placed vertically with the open and upward then find the length of the air column.
View Solution
Knowledge Check
An open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)A38 cmB6 cmC16 cmD22 cmAn open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. what will be length of the air column above mercury in the above now ?
(Atmospheric pressure = 76 cm of Hg)A38 cmB6 cmC16 cmD22 cmA vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
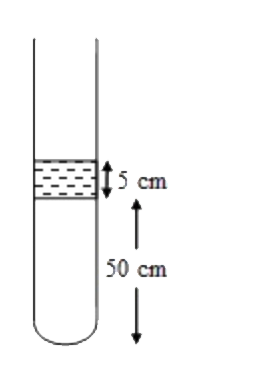 A56 cmB57 cmC60 cmD50 cm
A56 cmB57 cmC60 cmD50 cm
An open glass tube is immersed in mercury so that a length of 8cm of the tube projects above the mercury. The tube is then closed and raised through 44cm. What length of the tube will be occupied by the air after it has been raised? Given 1 atm =76cm of Hg.
View Solution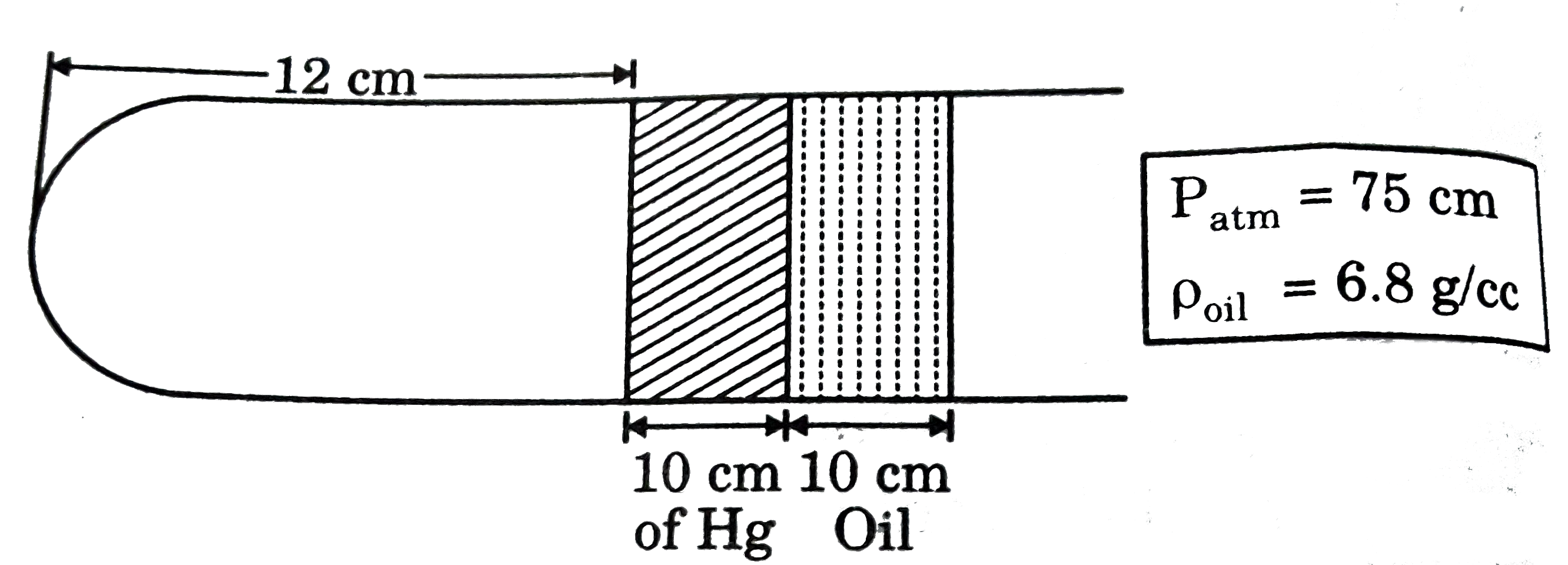
If above tube is held vertical with open end upward then find the length of air column (in cm).
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionA quill tube contains a mercury column of length 19cm. The length of air column is 24cm when it is held veritcally. On inverting it with its open end downwards the length of air column will be
(atmospheric pressure =76cm of Hg)
View SolutionSome mercury is poured into a capillary tube of uniform bore and one end closed. When the tube is held horizontally, mercury column has a length of 4 cm and air enclosed in the closed end has a length of 10 cm. If the tube is now held vertically, with open end upwards, the length of the air column will be (take atmospheric pressure at the place of experiment to be 760 mm)
View Solution
