A gas is enclosed in a cylinder with a movable frictionless piston. Its initial thermodynamic state at pressure Pi=105 Pa and volume Vi=10−3m3 changes to a final state at Pf=(1/32)×105PaandVf=8×10−3m3 in an adiabatic quasi-static process, such that P3V3=constant. Consider another thermodynamic process that brings the system form the same initial state to the same final state in two steps: an isobaric expansion at Pi followed by an isochoric (isovolumetric ) process at volume Vr. The amount of heat supplied to the system i the two-step process is approximately
112J
294J
588J
813J
The correct Answer is:C
To solve the problem, we need to find the amount of heat supplied to the system during a two-step process that takes the gas from its initial state to its final state. The two steps are an isobaric expansion followed by an isochoric process.
1. Identify the Given Values:
- Initial pressure, Pi=105Pa
- Initial volume, Vi=10−3m3
- Final pressure, Pf=132×105Pa=3.125×104Pa
- Final volume, Vf=8×10−3m3
2. Calculate Work Done in the Isobaric Process:
- The work done during an isobaric process (constant pressure) is given by:
Wisobaric=Pi(Vf−Vi)
- Substituting the values:
Wisobaric=105Pa×(8×10−3m3−10−3m3)=105×7×10−3=700J
3. Calculate Change in Internal Energy (ΔU):
- For an ideal gas, the change in internal energy during an isochoric process is given by:
ΔU=nCvΔT
- However, we can also use the first law of thermodynamics:
Q=ΔU+W
- Since we are considering the entire process, we need to find the total change in internal energy from initial to final state.
4. Calculate the Change in Internal Energy:
- The internal energy change during the adiabatic process can be calculated using:
ΔU=−Wadiabatic
- From the video transcript, we found that the work done during the adiabatic process is Wadiabatic=112.5J. Thus:
ΔU=−112.5J
5. Calculate the Total Heat Supplied:
- Using the first law of thermodynamics:
Qtotal=ΔU+Wisobaric
- Substituting the values:
Qtotal=−112.5J+700J=587.5J
Final Answer:
The amount of heat supplied to the system in the two-step process is approximately Q≈587.5J.
- Initial pressure, Pi=105Pa
- Initial volume, Vi=10−3m3
- Final pressure, Pf=132×105Pa=3.125×104Pa
- Final volume, Vf=8×10−3m3
- The work done during an isobaric process (constant pressure) is given by:
Wisobaric=Pi(Vf−Vi)
- Substituting the values:
Wisobaric=105Pa×(8×10−3m3−10−3m3)=105×7×10−3=700J
- For an ideal gas, the change in internal energy during an isochoric process is given by:
ΔU=nCvΔT
- However, we can also use the first law of thermodynamics:
Q=ΔU+W
- Since we are considering the entire process, we need to find the total change in internal energy from initial to final state.
- The internal energy change during the adiabatic process can be calculated using:
ΔU=−Wadiabatic
- From the video transcript, we found that the work done during the adiabatic process is Wadiabatic=112.5J. Thus:
ΔU=−112.5J
- Using the first law of thermodynamics:
Qtotal=ΔU+Wisobaric
- Substituting the values:
Qtotal=−112.5J+700J=587.5J
The amount of heat supplied to the system in the two-step process is approximately Q≈587.5J.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A gas take part in two thermal processes in which it is heated from the same initial state to the same final temperature. The processes are shown on the P−V diagram by straight lines 1→3 and 1→2
 AQ13<Q12BQ13>Q12CQ13=Q12DNone of above
AQ13<Q12BQ13>Q12CQ13=Q12DNone of aboveA gas take part in two thermal processes in which it is heated from the same initial state to the same final temperature. The processes are shown on the P−V diagram by straight lines 1→3 and 1→2
 AW13>W12BW12>W13CW13=W12DNone of above
AW13>W12BW12>W13CW13=W12DNone of aboveAn ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
AdU=0Bdθ=0Cdθ=dUDdw=dw
One mole of an ideal gas goes from an initial state A to final state B via two processes : It first undergoes isothermal expansion from volume V to 3V then its volume is reduced from 3V to V at constant pressure. The correct P-V diagram representing the two processes is
View SolutionOne mole of an ideal gas goes from an initial state A to final state B via two processs : It first undergoes isothermal expansion from volume V to 3V and then its volume is reduced from 3V to V at constant pressure. The correct P−V diagram representing the two process in (figure)
View SolutionOne mole of an ideal gas goes from an initial state A to final state B via two processs : It first undergoes isothermal expansion from volume V to 3V and then its volume is reduced from 3V to V at constant pressure. The correct P−V diagram representing the two process in (figure)
View SolutionAn ideal gas undergoes for different processes from the same initial state (figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4 which one is adiabatic ?
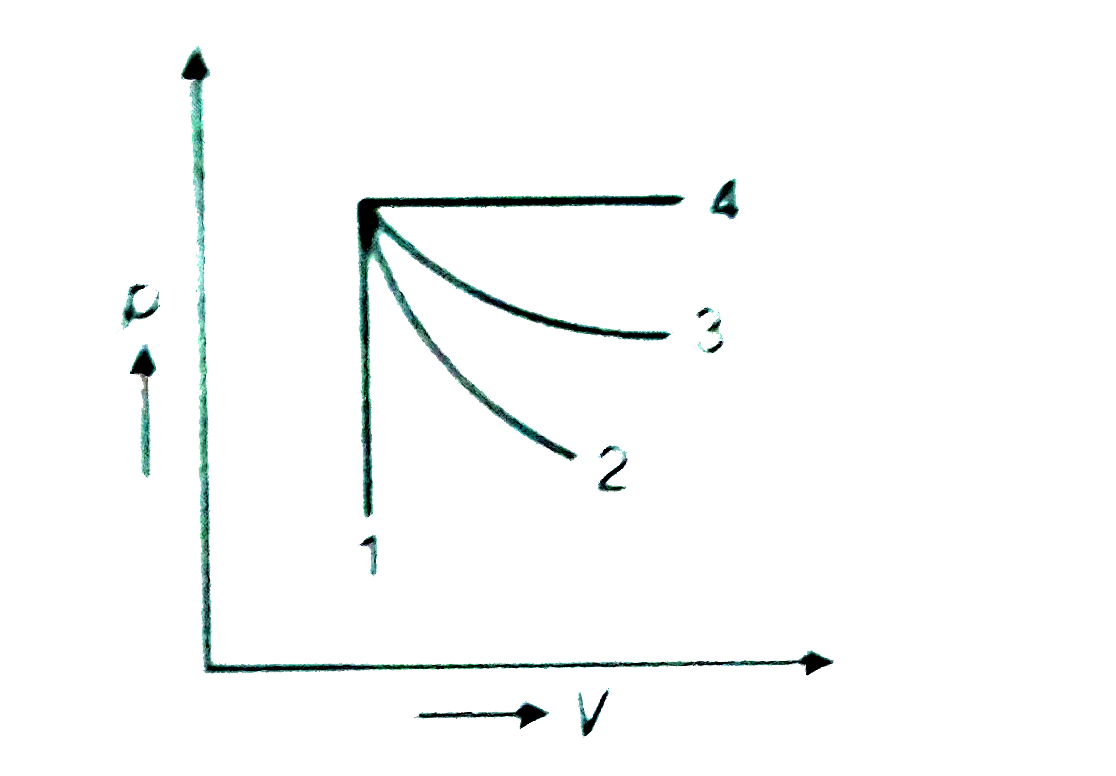
View Solutionconsider two processes on a system on a system as shown in
the volumes in the initial states are the same in the two processes and the volume in the final states are also the same.Let ΔW1andΔW2 be the work done by the sustem in the processes A and B respectively.

View Solution
