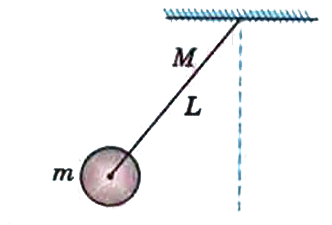
A metal rod of length 'L' and mass 'm' is pivoted at one end. A thin disc of mass 'M' and radius R <L is attached at its center to the free end of the rod. Consider two ways the disc is attached : (case A). The dise is not free to rotate about its centre and (case B) the disc is free to rotate about its centre. The rod disc system perfoms (SHM) in vertical plane after being released from the same displacement position. Which of the following statement (s) is (are) true ?
 .
.
Restoring torque in case A= Restoring torque in case (B).
restoring torque in case A lt Restoring torque in case (B).
Angular frequency for case A gt angular frequency for case (B).
Angular frequency for case A lt Angular frequency for case (B).
The correct Answer is:A, D
Apply∈gtau = I prop<br>Forcase(A):mg ((l)/(2) sin theta)) + Mg (l sin theta) = I_A prop_A<br>(##JMACHMOC10021_S01##).<br>Forcas(B):mg(l2sinθ))+Mg(lsinθ)=IB∝B
The restoring torque in both the cases is same.
AlsoIA>IB∴∝A<∝B
:. ωA<ωB
(a) and (d) are correct options.
Topper's Solved these Questions
Similar Questions
One end of a metal rod of length L and mass M is pivoted to a fixed support and to its free end, a thin disc of mass m and radius r (L) is attached at its centre. In one case, the disc is attached to the rod in such a way that it is not free to rotate about its centre and in another case, teh disc is free to rotate about its centre. When the rod-disc system is displaced slightly from its equilibrium position and released. it peforms S.H.M. in vertical plane. Compare the restoring torque acting on the system and angular frequency in both the cases.
View SolutionA uniform rod of mass M and length L with two particles m and m2 attached to its ends, is pivoted at its centre. The system rotates in a vertical plane with angular velocity ω.

View Solution
Knowledge Check
A metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R'(<L). Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
 ARestoring torque in case A = Restoring torque in caseBBRestoring torque in case A< Restoring torque in caseBCRestoring frequency case A> Angular frequency for caseBDRestoring frequency case A< Angular frequency for caseB
ARestoring torque in case A = Restoring torque in caseBBRestoring torque in case A< Restoring torque in caseBCRestoring frequency case A> Angular frequency for caseBDRestoring frequency case A< Angular frequency for caseBA metal rod of length 'L' and maws 'm' is pivoted at one end A thin disc of mass 'M' and radius 'R' ( Which of the folowing statement (s) is (are) true ?
 ARestoring torque in case A = Restoring torque in case BBRestorings torque in case A lt Restoring torque in case BCAngular frequency for case A gt Angular frequency for case B.DAngular frquency for case A lt Angular frequency for case B.
ARestoring torque in case A = Restoring torque in case BBRestorings torque in case A lt Restoring torque in case BCAngular frequency for case A gt Angular frequency for case B.DAngular frquency for case A lt Angular frequency for case B.A uniform thin rod of length 1m and mass 3 kg is attached to a uniform thin circular disc ois
A0.375 mB0.25mC0.125mD0.475m
Find the moment of inertia A of a spherical ball of mass m and radius r attached at the end of a straight rod of mass M and length l, if this system is free to rotate about an axis passing through the end of the rod (end of the rod opposite to sphere).

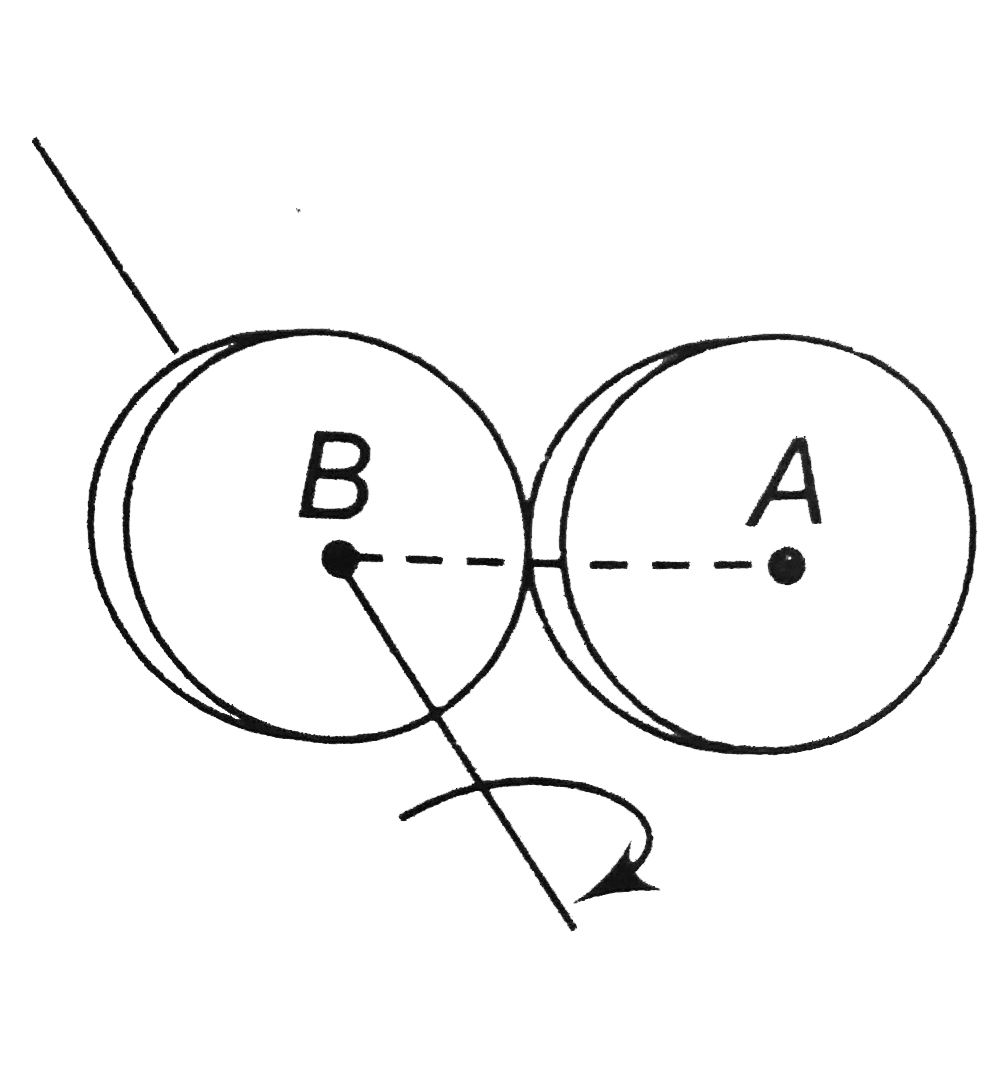
View SolutionTwo thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
 .
.
View SolutionA uniform thin rod of length 1m and mass 3kg is attached to a uniform thin circular disc of radius 30cm and mass 1kg at its centre perpendicular to its plane. The centre of mass of the combination from the centre of disc is
View SolutionA semicircular disc of mass M and radius R is free to rotate about its diameter. The moment of inertia of semicircular disc about a line perpendicular to its plane through centre is
View SolutionMoment of inertia of a thin rod of mass 'M' and length 'L' about the axis perpendicular to the rod and passing through its centre is ............
View Solution