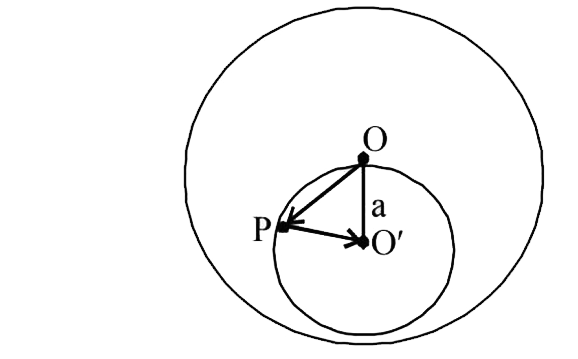
A spherical portion has been removed from a solid sphere having a charge distributed uniformly in its volume as shown in the figure. The electric field inisde the emptied space is

(a) zero everywhere
(b) non-zero and uniform
(c) non-uniform
(d) zero only at its center
The correct Answer is:B
Let us conisder a uniformly charged solid sphere without any cavity. Let the charge per unit volume be isgma and O be the centre of the sphere. Let us conisder a uniformly charged sphere of negative charged denisty isgma having its centre at O'. Also let OO' be equal to a. Let us conisder an arbitrary point P in the small sphere. The electric field due to charge on big sphere
→E1=isgma3eπslon0−−→OP
Also the electric field due to small sphere
→E2=isgma3eπslon0−−→PO' ∴ The total electric field
→E=→E1+→E2=isgma3eπslon0[−−→OP+−−→PO]=isgma3eπslon0−−→OO'
Thus electric field will have a finite value which will be uniform.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems
2 Videos
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions
2 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced
107 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
Similar Questions
Find the electric work done in bringing a charge q from A to B in a sphere of charge Q distributed uniformly throughout its volume.
 .
.
View SolutionA spherical conductor of radius 12 cm has a charge of 1.6×107 C distributed uniformly on its surface. What is the electric field
inside the sphere
(ii) just outside the sphere
© At a point 18 cm from the centre of the sphere?
View Solution
Knowledge Check
A very small sphere having a charge q, uniformly distributed throughout its volume, is placed at the vertex of a cube of side a. The electric flux through the cube is
Aqε0Bq3ε0Cq6ε0Dq8ε0A solid hemispherical uniformly charged body having charge Q is kept symmetrically along the y-axis as shown in the figure. The net electric field at (d, 0,0) is
 A14πε0Qd2Bless then 14πε0Qd2C>14πε0Qd2 and <14πε02Qd2D14πε02Qd2
A14πε0Qd2Bless then 14πε0Qd2C>14πε0Qd2 and <14πε02Qd2D14πε02Qd2A ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32
A spherical conductor of radius 12 cm has a charge of 1.6×10−7C distributed uniformly on its surface. What is the electric field (a) inside the sphere (b) just outside the sphere (c ) at a point 18 cm from the center of the sphere ?
View SolutionA spherical shell having charge +Q (uniformly distributed) and placed as shown. Find the force between shell and the point charge (r>>R).

View SolutionFind the electric field at an arbitrary point of a sphere carrying a charge uniformly distributed over its volume.
View SolutionA spherical conductor of radius 12 cm has charge of 1.6×10−7C distributed uniformly on its surface. What is the electric field
(a) inside the sphere (b) just outside the sphere
(c ) at a point 18 cm from the centre of the spere ?
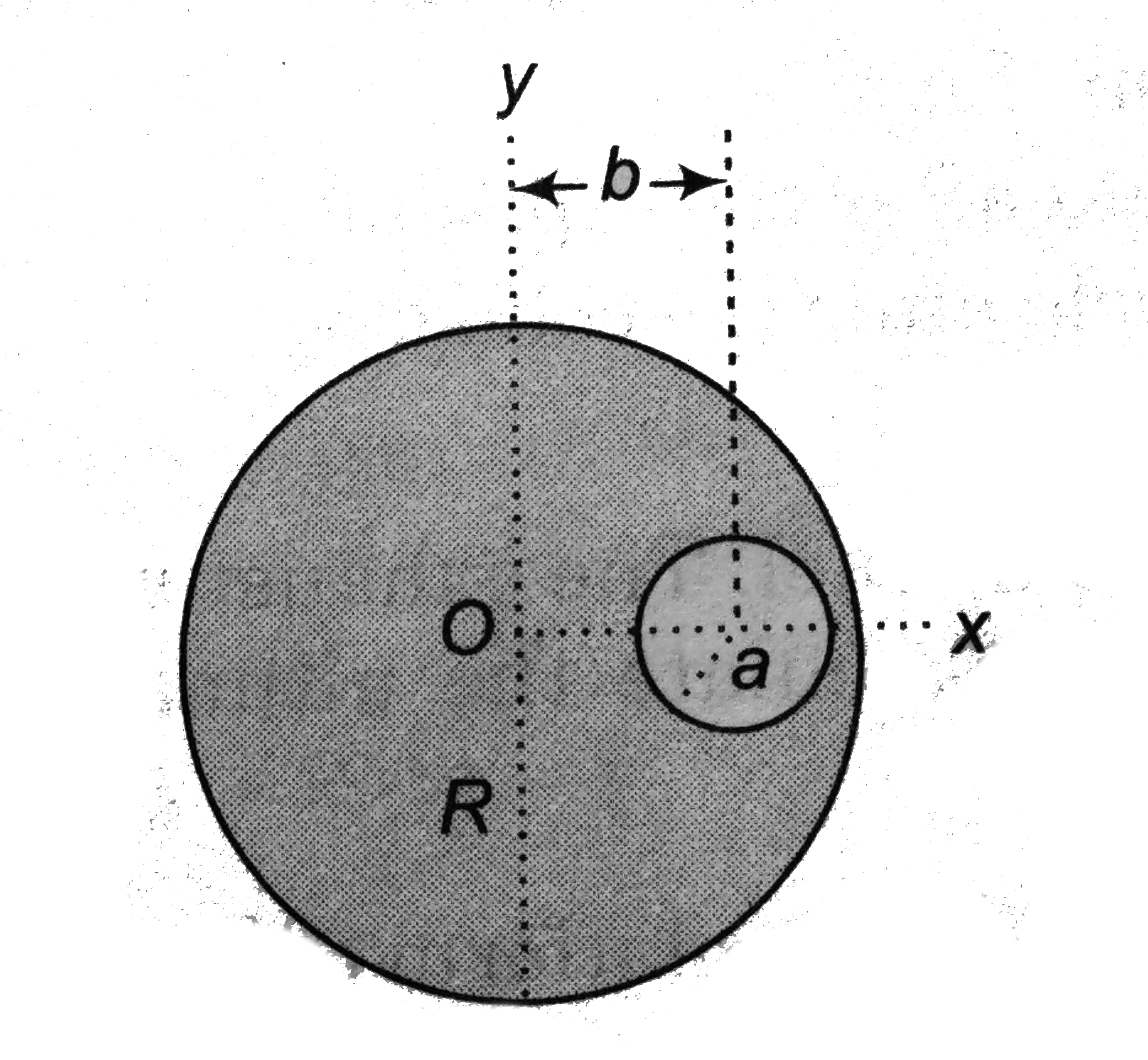
View SolutionThe uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
View Solution
