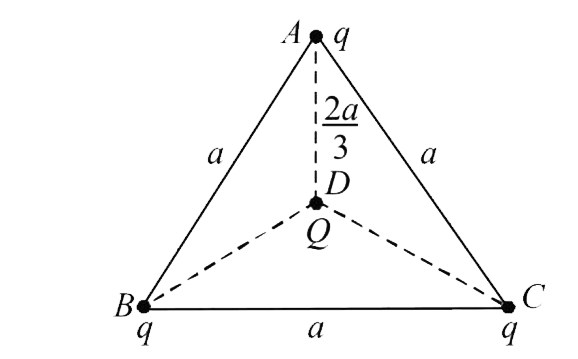
Three charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the center of the triangle.
a. Find the net force on charge q.
b. If Q=−q, will the charges at the corners move toward the center or fly away from it ?
c. For what value of Q and O will the charges remain stationary ?
d. In situation (c), how much work is done in removing the charges to infinity ?
The correct Answer is:A, B, C, D
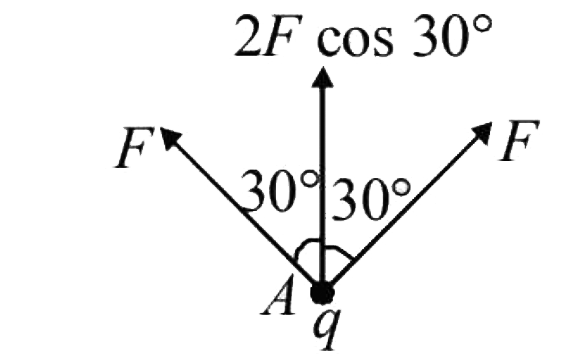
(i) The force on charge q kept at A due to charges kept at B and C
F1=2Fcos30∘
F1=√3×(9×109q2a2)
The force on q due to charge (−q) kept at D
F2=9×109q2(2a/3)2=94×(9×109×q2a2)
Clearly the two forces are not equal. Also as F2>F1 the charges will move towards the centre.
(ii) For charges to remain stationary
2×Kq2a2×√32=94×K×q2Qa2⇒4√3q9=Q
The charge Q should be negative.
The potential energy of the system is
=3[Kq2a2+Kq2a2]+3[K×4√39q×q(2a/3)2]
=6K×q2a2+3√3Kq2a2=3(2+√3)Kq2a2
This is the amount of work needed to move the charges to infinity.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems
2 Videos
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions
2 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced
107 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
Similar Questions
Three charges, each of value q, are placed at the vartices of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. (i) If Q=−q, will the charge at the vertices move towards the centre of fly away from it? (ii) For what value of Q will the charges remain stationary?
View SolutionThree charges, each of value q, are placed at the comers of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. If the value of Q for which charges remain stationary is (−q√n), then find n.
View Solution
Knowledge Check
Three charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. If Q=−q:
Athe charges will move towards the centreBthe charges will move away from the centreCthe charges will remain stationaryDthe charges may move in any directionThree equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
Akq/r2B3kq/r2C√3kq/r2DzeroThree charges each of magnitude q are placed at the corners of an equilateral triangle, the electrostatic force on the charge place at the centre is (each side of triangle is L)
 AZeroB14πε0q2L2C14πε03q2L2D112πε0q2L2
AZeroB14πε0q2L2C14πε03q2L2D112πε0q2L2
Three charges +q,+qand−q are located at the corners of an equilaterial triangle of side a. Calculate potential energy of the system.
View SolutionThree charges +Q each are placed at the corners A,B and C of an equilateral triangle. At the circumcenre, O the electric field wil be

View SolutionThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
View SolutionThree charge +Q,+Q and −Q are placed at the corners of an equilateral triangle. The ratio of the force on a positive charge to the force on the negative charge will be equal to
View SolutionThree charge −q,+q and −q are placed at the cornors of an equilateral triangle of side a The resultant electric froce an a charge +q placed at a the centroid O of the triangle is
View Solution
