Three charge −q,+q and −q are placed at the cornors of an equilateral triangle of side a The resultant electric froce an a charge +q placed at a the centroid O of the triangle is
3q24πε0a2
q24πε0a2
q22πε0a2
3q22πε0a2
The correct Answer is:4
To solve the problem of finding the resultant electric force on a charge +q placed at the centroid O of an equilateral triangle with charges −q,+q,−q at its corners, we can follow these steps:
Step 1: Identify the Geometry
We have an equilateral triangle with three charges:
- Charge −q at point A
- Charge +q at point B
- Charge −q at point C
The centroid O of the triangle is the point where we will place the charge +q.
Step 2: Calculate the Distance from the Centroid to the Corners
The distance from the centroid O to any vertex (corner) of the triangle can be calculated using the formula:
r=a√3
where a is the side length of the triangle.
Step 3: Calculate the Electric Forces Due to Each Charge
The electric force F between two point charges is given by Coulomb's law:
F=k|q1q2|r2
where k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and r is the distance between them.
For the charge +q at the centroid O:
1. Force due to charge at A (−q):
FA=k|−q⋅+q|r2=kq2(a√3)2=k3q2a2
This force is attractive and directed towards charge −q at A.
2. Force due to charge at B (+q):
FB=k|+q⋅+q|r2=kq2(a√3)2=k3q2a2
This force is repulsive and directed away from charge +q at B.
3. Force due to charge at C (−q):
FC=k|−q⋅+q|r2=kq2(a√3)2=k3q2a2
This force is attractive and directed towards charge −q at C.
Step 4: Resolve Forces into Components
Since the triangle is equilateral, we can resolve the forces into components. The angle between the line connecting the centroid to the vertex and the horizontal axis is 30∘ for charges at A and C, and 60∘ for charge B.
- Force components:
- For FA and FC:
- Horizontal components: FAcos(30∘) and FCcos(30∘)
- Vertical components: FAsin(30∘) and FCsin(30∘)
- For FB:
- Horizontal component: FB
- Vertical component: 0
Step 5: Calculate the Resultant Force
The net force in the horizontal direction will cancel out due to symmetry, while the vertical components will add up.
The total vertical force Fnet will be:
Fnet=FAsin(30∘)+FCsin(30∘)−FB
Substituting the values:
Fnet=2⋅k3q2a2⋅12−k3q2a2
This simplifies to:
Fnet=0
Final Result
The resultant electric force on the charge +q placed at the centroid O is:
Resultant Electric Force=0
We have an equilateral triangle with three charges:
- Charge −q at point A
- Charge +q at point B
- Charge −q at point C
The distance from the centroid O to any vertex (corner) of the triangle can be calculated using the formula:
r=a√3
where a is the side length of the triangle.
The electric force F between two point charges is given by Coulomb's law:
F=k|q1q2|r2
where k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and r is the distance between them.
1. Force due to charge at A (−q):
FA=k|−q⋅+q|r2=kq2(a√3)2=k3q2a2
This force is attractive and directed towards charge −q at A.
FB=k|+q⋅+q|r2=kq2(a√3)2=k3q2a2
This force is repulsive and directed away from charge +q at B.
FC=k|−q⋅+q|r2=kq2(a√3)2=k3q2a2
This force is attractive and directed towards charge −q at C.
Since the triangle is equilateral, we can resolve the forces into components. The angle between the line connecting the centroid to the vertex and the horizontal axis is 30∘ for charges at A and C, and 60∘ for charge B.
- For FA and FC:
- Horizontal components: FAcos(30∘) and FCcos(30∘)
- Vertical components: FAsin(30∘) and FCsin(30∘)
- Horizontal component: FB
- Vertical component: 0
The net force in the horizontal direction will cancel out due to symmetry, while the vertical components will add up.
Fnet=FAsin(30∘)+FCsin(30∘)−FB
Substituting the values:
Fnet=2⋅k3q2a2⋅12−k3q2a2
This simplifies to:
Fnet=0
The resultant electric force on the charge +q placed at the centroid O is:
Resultant Electric Force=0
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level II(C.W)
27 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level III (C.W)
55 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - C.U.Q
133 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS
14 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
Similar Questions
Three charges -q +q and +q are placed at the corner of the equilateral triangle of side a as shown in the figure.The net electric potential at the centroid of the triangle will be (k=(1)/(4 pi varepsilon_(0)))
View SolutionThree charges +q,+qand−q are located at the corners of an equilaterial triangle of side a. Calculate potential energy of the system.
View Solution
Knowledge Check
Three charges q1,q2,q3 each equal to q placed at the vertices of an equilateral triangle of side l . What will be the force on a charge Q placed at the centroid of triangle ?
A4NB5NC10NDZeroThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.Three point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A(√34πε0)(qa)2B(√24πε0)(qa)2C(√34πε0)(q2a)2D(√24πε0)(2qa)2
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionThree identical charges of q each are placed at the three verticess of an equilateral triangle ABC of side a, Electrostatic force experienced by a point charge q0 situated at the centroid G of triangle is ___________
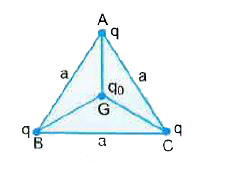
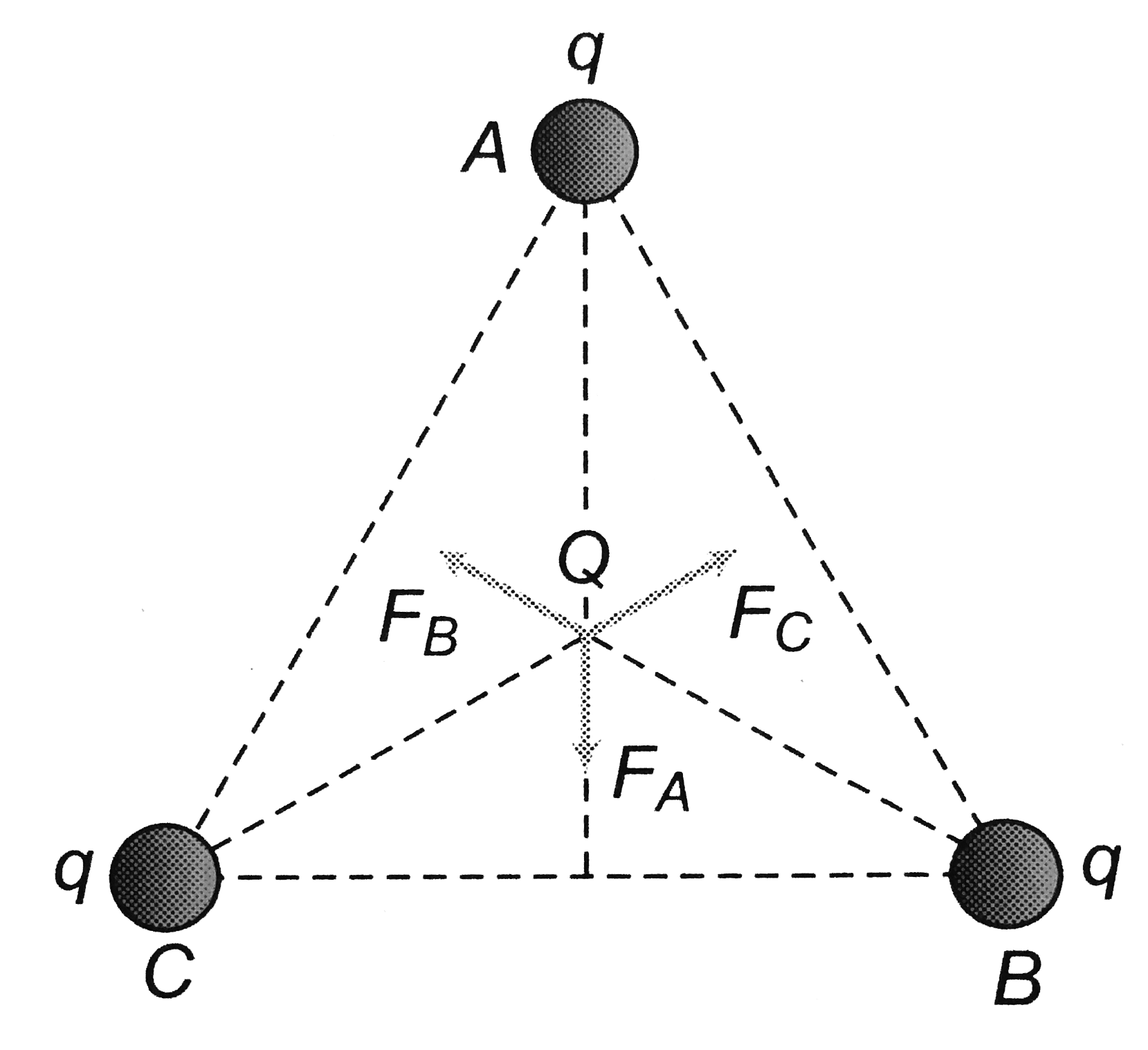
View SolutionThree charges each of magnitude q are placed at the corners of an equilateral triangle, the electrostatic force on the charge place at the centre is (each side of triangle is L)
View Solutionthree points charges are placed at the cornors of an equilibrium triangle of side L as shown in the figure
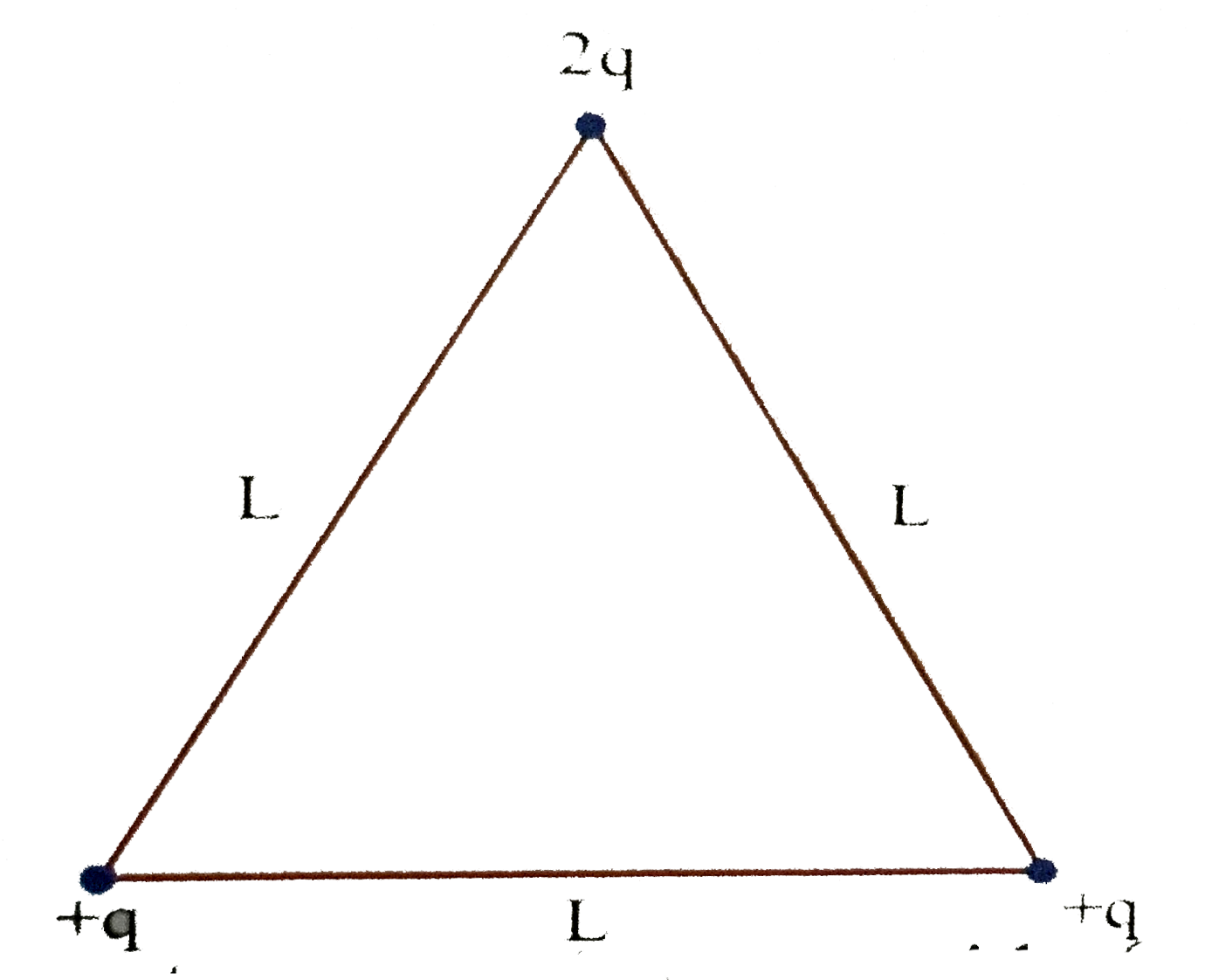
View SolutionElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View Solution
