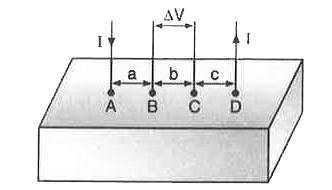
Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
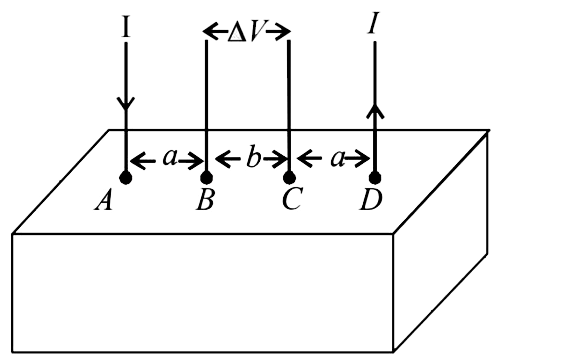
Delta V measured between B and C is
ρIπa−ρIπ(a+b)
ρIa−ρIa+b
ρI2πa−ρI2π(a+b)
ρI2π(a−b)
The correct Answer is:A
(a) Let j be the current density.
Then j×2πr2=I⇒j=I2πr2∴E=ρj=ρI2πr2
Now, ΔV'BC=−∫aa+b→E.→dr=−∫aa+bρI2πr2dr
=−ρl2π[−1r]aa+b=ρI2πa−ρI2π(a+b)
On applying superposition as mentioned we get
ΔVBC=2×ΔV'BC=ρIπa−ρIπ(a+b).
Topper's Solved these Questions
Similar Questions
A uniform wound solenoidal coil of self inductance 1.8×10−4 henry and resistance 6 ohm is broken up into two identical coils. These identical coils are then connected in parallel across a 15-volt battery of negligible resistance. The time constant for the current in the circuit is.......seconds and the steady state current through the battery is ..............amperes.
View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View SolutionConsider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
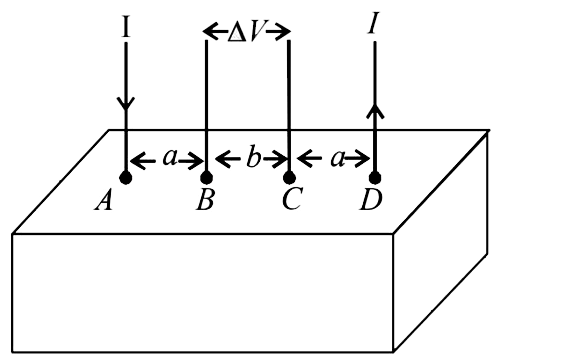
For current entering at A, the electric field at a distance 'r'
View SolutionCurrent I enters at A in a square loop of uniform resistance and leaves at B. The ratio of magnetic field at E, the centre of square, due to segment AB to that due to DC is

View Solutionसलग्न चित्र में प्रदर्शित परिपथ के लिए ज्ञात कीजिए -
(i) प्रतिबाधा ,
(ii) शक्ति गुणांक ,तथा
(iii) धारा एवं वोल्टता के बीच कलांतर ।
View Solutionसंलग्न चित्र में प्रदर्शित परिपथ की- (i) प्रतिबाधा, (ii) शक्ति गुणांक तथा (iii) धारा व वोल्टता के बीच कलान्तर की गणना कीजिए।
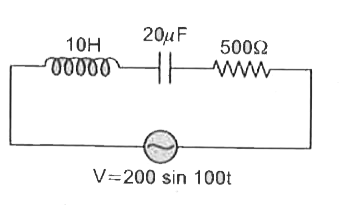
View Solutionपैरा 4
चित्र II.75 में दिखाया गया ρ प्रतिरोधकता वाला चालक पदार्थ का एक गुटका लें। धारा I, बिन्दु A से प्रवेश करती है और D से बाहर निकलती है। हम अध्यारोपण का नियम लगाकर B और C के बीच पैदा हुई वोल्टता ΔV निकालते हैं। यह इन चरणों में किया जाता है :
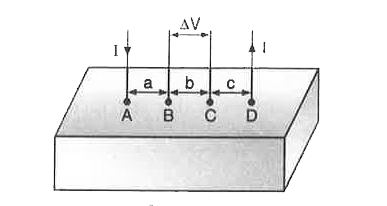
(i ) मान लें कि धारा, I, बिन्दु A से प्रवेश करती हैं और गुटके में एक गोलार्ध पृष्ठ पर फैली हुई है।
(ii) A से r दुरी पर क्षेत्र E(r) ओम का नियम E=ρj प्रयुक्त करते हुए निकालें जहाँ j, r दूरी पर प्रति यूनिट क्षेत्रफल धारा है। की पर निर्भरता से पर विभव V (r) निकालें।
(iv) D से निकल रही धारा I के लिए (i), (ii) और (iii) को दोहराएँ औरA और D के लिए परिणामों का अध्यारोपण करें।
B और C के बीच मापा गया ΔV है
View Solutionपैरा 4
चित्र II.75 में दिखाया गया ρ प्रतिरोधकता वाला चालक पदार्थ का एक गुटका लें। धारा I, बिन्दु A से प्रवेश करती है और D से बाहर निकलती है। हम अध्यारोपण का नियम लगाकर B और C के बीच पैदा हुई वोल्टता ΔV निकालते हैं। यह इन चरणों में किया जाता है :
(i ) मान लें कि धारा, I, बिन्दु A से प्रवेश करती हैं और गुटके में एक गोलार्ध पृष्ठ पर फैली हुई है।
(ii) A से r दुरी पर क्षेत्र E(r) ओम का नियम E=ρj प्रयुक्त करते हुए निकालें जहाँ j, r दूरी पर प्रति यूनिट क्षेत्रफल धारा है। की पर निर्भरता से पर विभव V (r) निकालें।
(iv) D से निकल रही धारा I के लिए (i), (ii) और (iii) को दोहराएँ औरA और D के लिए परिणामों का अध्यारोपण करें।
A पर प्रवेश करने वाली धारा के लिए A से r दूरी पर विद्युत क्षेत्र है
View SolutionIn the picture rho A driver of resistivity is the block. Entering section A and coming out of D. We generate the potential difference between B and C. DeltaV To make known, we apply the principle of imposition. The calculation is done in the following steps (i) I take the stream entering from A and assume that inside the block it spreads on a semicircular surface. (ii) Ohm's law E=rhoJ , Where J is the current flowing through the unit area, find the electric field E (r) at a distance from A to r. (iii) Determine the potential V (r) at r distance from the dependence of E (r) on r. (iv) Repeat the terms (i), (ii) and (iii) issued on D for Section I and use the result on A and D. For the current entering A, the electric field at a distance from A to r
View Solutionआरेख में दर्शाए प्रतिरोधकता 'ρ' के चालक पदार्थ से बने किसी गुटके परविचार कीजिए। धारा 'I', 'A' पर प्रवेश करती है तथा 'D' से निकलती है। 'B' तथा 'C' के बीच विकसित वोल्टता 'ΔV' को ज्ञात करने के लिए हम अध्यारोपण सिद्धांत का अनुप्रयोग करते हैं। इसमें परिकलन निम्नलिखित चरणों में किए गए हैं।
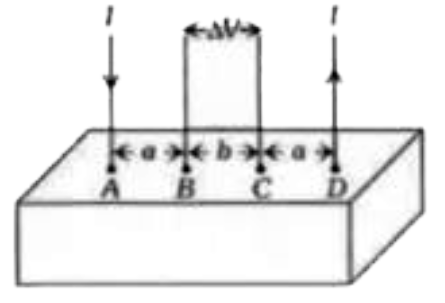
(i) धारा 'I' को 'A' से प्रवेश करते हुए लीजिए तथा यह मानिए कि यह गुटके में अर्धगोलीय पृष्ठ पर फैल जाती है।
(ii) बिन्दु A से दूरी 'r' पर विद्युत-क्षेत्र E(r) का परिकलन ओम के नियम E=ρj, जहाँ j, दूरी 'r' पर धारा प्रति एकांक क्षेत्रफल है, का उपयोग करके कीजिए।
(iii) E (r) की 'r' पर निर्भरता द्वारा r पर विभव V(r) प्राप्त कीजिए।
(iv) 'D' पर धारा 'I' निकालने के लिए चरणों (i), (ii) तथा (iii) को दोहराइए तथा 'A' तथा 'D' के परिणामों का अध्यारोपण कीजिए।
A पर धारा के प्रवेश के लिए, A से 'r' दूरी पर विद्युत-क्षेत्र है
View SolutionAs shown in the figure 'rho' Consider a block of resistive conductive material. Section 'I' flows through 'A' and gets expelled from 'D'. We originated between 'B' and 'C' Delta V The principle of imputation is used to find the voltage. The calculation is done in the following terms. : (i) Assume Section 'I' entering from A and assume that it spreads above the semicircular surface in the block. (ii) Ohm's law E=rho j Calculate the electric field E (r) at the distance from A to r using the area j per unit area on 'r'. (iii) The dependence of E (r) on r gives the potential V (r) at r. (iv) Repeat (i), (ii) and (iii) for Section I issued from D and install the results for A and D. For the current entering from A, the electric field at the distance 'r' from A is -
View SolutionAs shown in the figure 'rho' Consider a block of resistive conductive material. Section 'I' flows through 'A' and gets expelled from 'D'. We originated between 'B' and 'C' Delta V The principle of imputation is used to find the voltage. The calculation is done in the following terms. : (i) Assume Section 'I' entering from A and assume that it spreads above the semicircular surface in the block. (ii) Ohm's law E=rho j Calculate the electric field E (r) at the distance from A to r using the area j per unit area on 'r'. (iii) The dependence of E (r) on r gives the potential V (r) at r. (iv) Repeat (i), (ii) and (iii) for Section I issued from D and install the results for A and D. Measured between B and C Delta V is -
View SolutionCurrent I enters at A in a square loop of uniform resistance and leaves at B. The ratio of magnetic field at E, the centre of square, due to segment AB to that due to DC is

View SolutionConsider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.

Delta V measured between B and C is
View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View Solution
