LetC be the capacitance of a capacitor discharging through a resistor R. Suppose is the time taken for the energy stored in the capacitor to reduce to half its initial value and is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio will be
1
2
The correct Answer is:C
To solve the problem, we need to find the ratio t1t2, where t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value, and t2 is the time taken for the charge to reduce to one-fourth its initial value.
Step 1: Understand the formulas for energy and charge in a capacitor
The energy U stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
The charge Q on a capacitor is given by:
Q=CV
Step 2: Determine the time t1 for energy to reduce to half
When the capacitor discharges through a resistor, the voltage across the capacitor decreases exponentially:
V(t)=V0e−tRC
where V0 is the initial voltage, R is the resistance, and C is the capacitance.
The energy at time t is:
U(t)=12C(V(t))2=12C(V0e−tRC)2=12CV20e−2tRC
To find t1, we set U(t1)=12U0:
12CV20e−2t1RC=12(12CV20)
This simplifies to:
e−2t1RC=12
Taking the natural logarithm of both sides:
−2t1RC=ln(12)
Thus,
t1=−RC2ln(12)=RC2ln(2)
Step 3: Determine the time t2 for charge to reduce to one-fourth
The charge on the capacitor also decreases exponentially:
Q(t)=Q0e−tRC
where Q0=CV0.
To find t2, we set Q(t2)=14Q0:
Q0e−t2RC=14Q0
This simplifies to:
e−t2RC=14
Taking the natural logarithm of both sides:
−t2RC=ln(14)
Thus,
t2=−RCln(14)=RCln(4)
Step 4: Find the ratio t1t2
Now we can find the ratio:
t1t2=RC2ln(2)RCln(4)=12⋅ln(2)ln(4)
Since ln(4)=ln(22)=2ln(2):
t1t2=12⋅ln(2)2ln(2)=14
Final Answer
The ratio t1t2 is:
t1t2=14
The energy U stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
Q=CV
When the capacitor discharges through a resistor, the voltage across the capacitor decreases exponentially:
V(t)=V0e−tRC
where V0 is the initial voltage, R is the resistance, and C is the capacitance.
U(t)=12C(V(t))2=12C(V0e−tRC)2=12CV20e−2tRC
12CV20e−2t1RC=12(12CV20)
This simplifies to:
e−2t1RC=12
Taking the natural logarithm of both sides:
−2t1RC=ln(12)
Thus,
t1=−RC2ln(12)=RC2ln(2)
The charge on the capacitor also decreases exponentially:
Q(t)=Q0e−tRC
where Q0=CV0.
Q0e−t2RC=14Q0
This simplifies to:
e−t2RC=14
Taking the natural logarithm of both sides:
−t2RC=ln(14)
Thus,
t2=−RCln(14)=RCln(4)
Now we can find the ratio:
t1t2=RC2ln(2)RCln(4)=12⋅ln(2)ln(4)
Since ln(4)=ln(22)=2ln(2):
t1t2=12⋅ln(2)2ln(2)=14
The ratio t1t2 is:
t1t2=14
Topper's Solved these Questions
Similar Questions
In a chrging cirucit, after how many time constant will the energy stored in the capacitor reach one - half of its equilibrium value?
View SolutionA capacitor with initial charge q0, is discharged through a resistor. What multiple of the time constant τ gives the time the capacitor takes to lose (a) the first 25% of its charge and (b) 50% of its charge?
View Solution
Knowledge Check
A charged capacitor of capacitance C is discharging through a resistor of resistance R. At what time the charge on the capacitor is equal to one half of its initial value?
ARC2BRCloge2CRC loge2D1RCloge2In a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
A(ln2)LRB0.5LRC√2LRD(√2√2−1)LRA charged capacitor is connected with a resistor. After how many time constants, does the energy of capacitor (1100)th becomes of its initial value?
A2.3B1.15C0.69D4.6
A parallel plate capacitor of 1μF capacity is discharging thorugh a resistor. If its energy reduces to half in one second. The value of resistance will be
View SolutionA capacitor discharges through a resistance. The stored energy U0 in one capacitive time constant falls to
View SolutionThe capacitor of capacitance C in the circuit shown in fully charged initially. Resistance is R.–
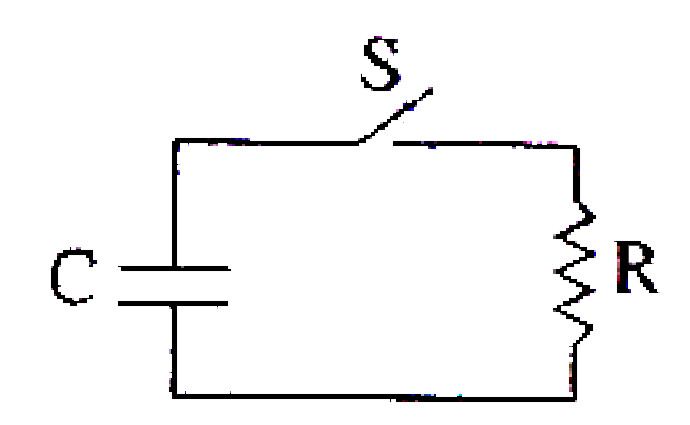
After the switch S is closed, the time taken to reduce the stored energy in the capacitor to half its initial value is
View SolutionWhen the uncharged capacitor is charged through a resistor 'R' by a battery of emf 'epsilon’' as shown, the time taken to get charge that is 50% of the equilibrium value would be
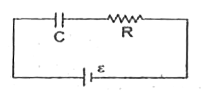
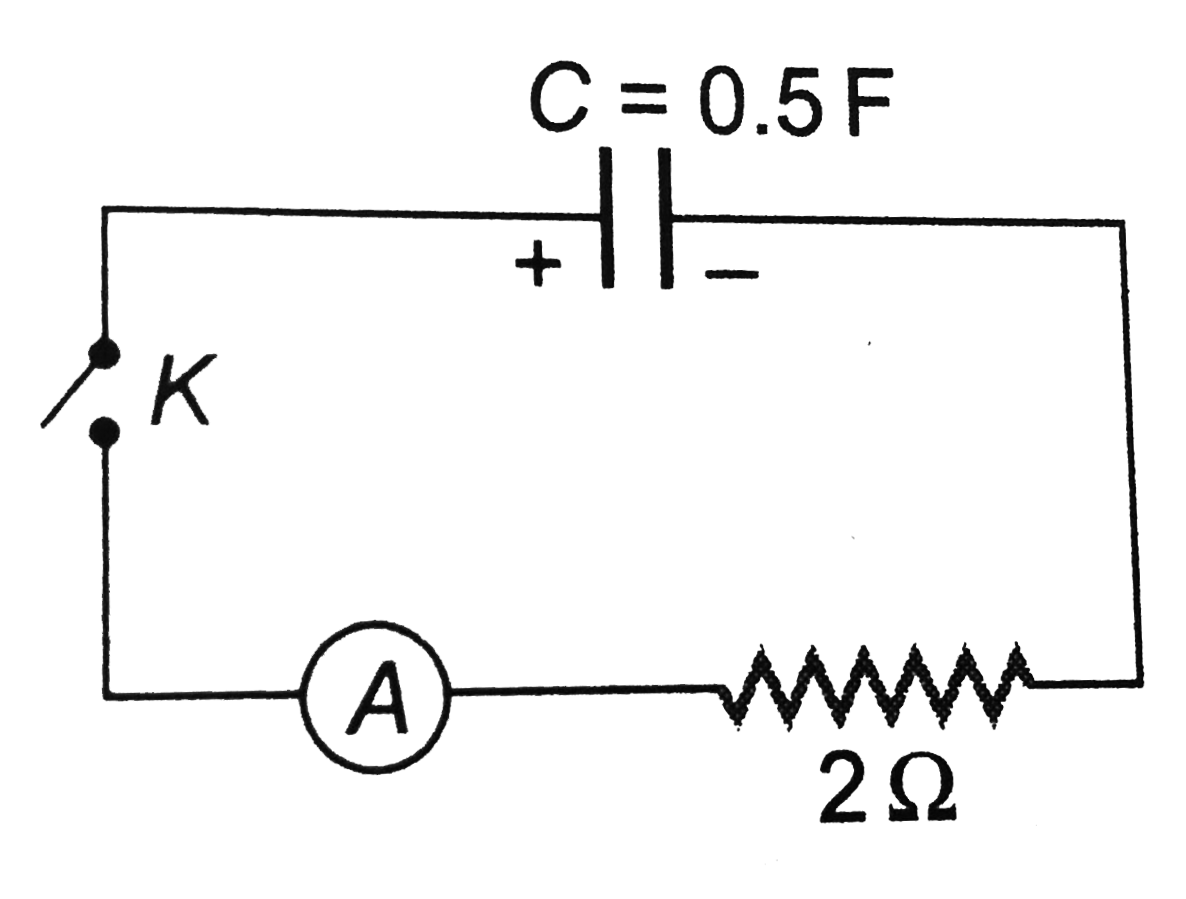
View SolutionA charged capacitor is allowed to dischare through a resistor by closing the key at the instant t=0. At the instant t=(ln4)μs, the reading of the ammeter falls half the initial vaslue. The resistance of the ammeter is equal to
View Solution