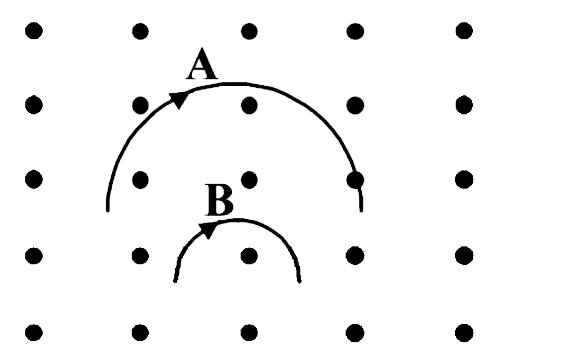
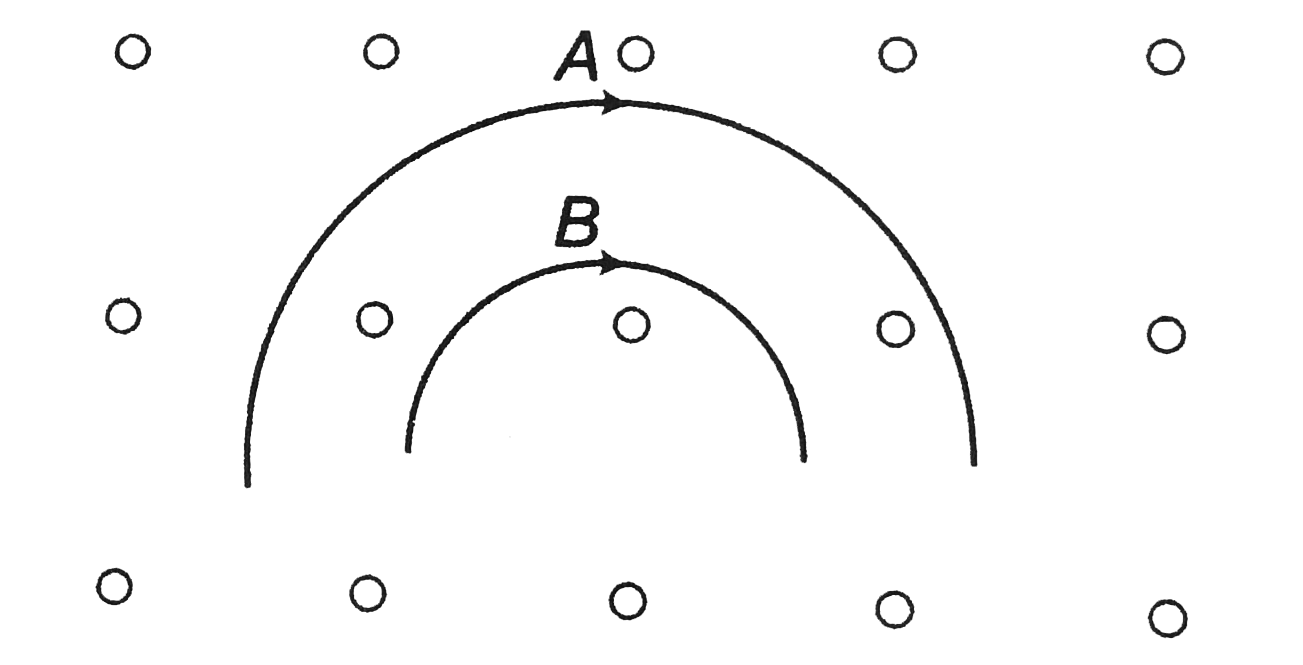
Two particles AandB of masses mAandmB respectively and having the same charge are moving in a plane . The speeds of the particles are vAandvB respectively and the trajectories are as shown in the figure. Then
mAvA<mBvB
mAvA>mBvB
mAvA<mBandvA<vB
mA=mBandva=vB
The correct Answer is:B
KEY COCNCEPT: When a charged particle is moving at right angles to the magnetic field then a force acts on it which behaves as a centripetal force and moves the particle in circular motion .
:. mAv2ArA=q.vAB∴mAvArA=qB
mBvBrB=qB
rArr mAvArA=mBvBrB
rA>rB
rArr m_(A)v_(A) gt m_(B) v_(B)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - MCQs(d )
1 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
- RAY AND WAVE OPTICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - RAY AND WAVE OPTICSEXERCISE - JEE Main And Advanced
209 Videos
Similar Questions
Two particles A and B of masses m and 2m have charges q and 2q respectively. Both these particle moving with velocities v1andv2 respectively in the same direction enter the same magnetic field B acting normally to their direction of motion. If the two force FAandFB acting on them are in the ratio 1:2 , find the ratio of their velocities.
View SolutionTwo particles A & B of mass m1 and m2 respectively start moving from O with speeds v1, and v2. A moves towards the plane mirror and B moves parallel to mirror horizontally. The mirror is in y-z plane. The absolute-speed of image of centre of mass of the system (image of A + image of B)is:
View Solution
Knowledge Check
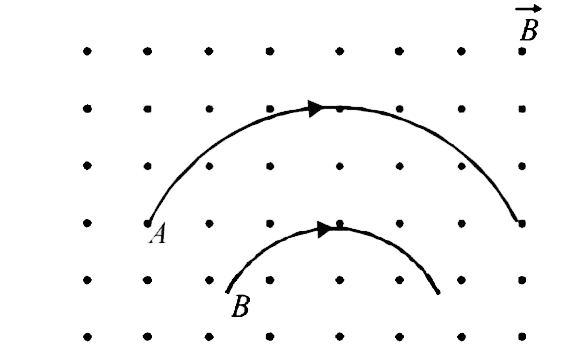
Two particle A and B of masses mA and mB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vA and vB respectively and the trajectories are as shown in the figure. Then-
 AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vB
AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vBTwo particles A and B of masses mAandmB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vAandvB respectively and the trajectories are as shown in the figure. Then -
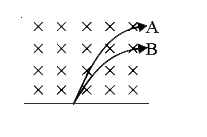 AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vB
AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vBTwo particles A and B of masses mA and mB respectively and having the same charge are moving ina plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vA and vB respectively and the trajectories are as shown in the figure. Then,
 AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vB
AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vB
Two particles A and B with particle A having mass m, are moving towards each other under their mutual force of attraction. If their speeds at certain instant are v and 2v respectively, then find the K.E. of the system.
View SolutionThe answer to each of the following questions is a single-digit integer ranging from 0 to 9. Darken the correct digit.
There is one particle A having charge q and mass m. There is another particle B of charge eight times and mass two times to that of A. Both the particles are accelerated through the same potential difference. Let speeds acquired by the particles A and B be vA and vB respectively, then calculate vB/vA.
View SolutionTwo particles A and B of masses 10 kg and 38 kg, respectively, are moving along the same straight line with velocities 15 m/s and 3 m/s, respectively, in the same direction. After elastic collision, the velocities of A and B are vAand vB, respectively, in the direction of initial motion. Then
View SolutionParticle A makes a perfectly elastic collision with anther particle B at rest. They fly apart in opposite direction with equal speeds. If the masses are mA&mB respectively, then
View SolutionTwo particles A and B of mass m each hit the ends of a rigid bar of mass M and length l inelastically from opposite sides the speeds v and perpendicular to the rod. The bar is kept on a smooth horizontal plane (as shown). Find the linear and angular speed of the system (bar+particle).

View Solution
