A biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
virtual and at a distance of 16 cm from the mirror
real and at a distance of 16 cm from the mirror
virtual and at a distance of 20 cm from the mirror
real and at a distance of 20 cm from the mirror
The correct Answer is:B
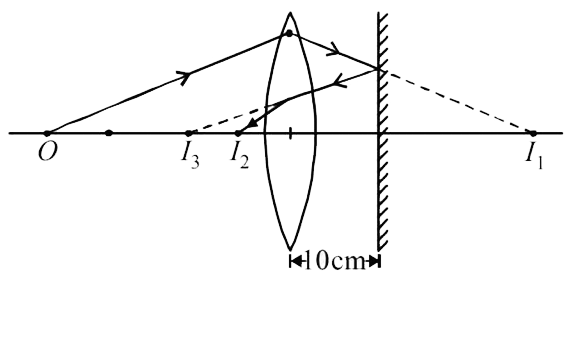
Focal length of the biconvex lens is 15 cm. A small object is placed at a distance of 30cm from the lens i.e. at a distance of 2f. Therefore the image should form at But since the ray strike the plane mirror before reaching I1, The image I_(1) acts as the virtual object for reflection on plane mirror kept at a distance of 20 cm from it. It should produce an image I_(2) but as the ray encounters the lens, it gets refracted and the final image is formed at I_(3). For the last refraction from the biconvex lens, u=10cm.
Applying lens formuls 1v−1u=1f
⇒ 1v=110=115 ⇒ 1v=115+110=25150
⇒ v=6cm
Therefore a real image is formed at a distance of 16cm from the plane mirror.
Topper's Solved these Questions
Similar Questions
A convex lens of focal length 15cm is placed in front of a convex mirror. Both are coaxial and the lens is 5cm from the apex of the mirror. When an object is placed on the axis at a distance of 20cm from the lens, its is found that image coincides with the object. Calculate the radius of curvature of mirror.
[55cm]
View SolutionA convex lens is placed coaxially near a convex mirror of radius of curvature 30 cm. the distance between the lens and the mirror is 40 cm. Calculate the focal length of the lens if the final image of an object placed at 35 cm coincide with the object itself.
View Solution
Knowledge Check
A biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
AVirtual and at a distance of 16 cm from the mirrorBReal and at a distance of 16 cm from the mirrorCVirtual and at the distance of 20 cm from the mirrorDNone of the aboveA biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
Avirtual and at a distance of 16 cm from the mirrorBreal and at a distance of 16cm from the mirrorCvirtual and at a distance of 20cm from the mirrorDreal and at a distance of 20cm from the mirrorA convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
A thin convex lens of focal length 'f' is put on a plane mirror as shown in the figure . When an object is kept at a distance 'a' from the lens - mirror combination , its image is formed at a distance a3 in front of the combination . The value of 'a' is :-
_E01_189_Q01.png)
View SolutionA convex lens of focal length 15 cm is placed on a plane mirror. An object is placed 20 cm from the lens. The image is formed
View SolutionA convex lens of focal length 30 cm , a concave lens of focal length 120 cm , and a plane mirror are arranged as shown . For an object kept at a distance of 60 cm from the convex lens, the final image, formed by the combination , is a real image , at a distance of :
_E01_195_Q01.png)
|Focal length|=|Focal length|
= 30cm =120cm
_S01_267_Q02.png)
View SolutionAn object is placed in front of a thin convex lens of focal length 30cmand a plane mirror is placed15cmbehind the lens.If the final image of the object coincides with the object the distance of the object from the lens is
View SolutionA convex lens of focal length 15 cm is placed in front of a plane mirror at a distance 25 cm from the mirror. Where on the optical axis and from the centre of the lens should a small object be placed such that the final image coincides with the object ?
View Solution