A rubber ball is dropped from a height of 5mon a plane, where the acceleration due to gravity is not shown. On bouncing it rises to 1.8m. The ball loses its velocity on bouncing by a factor of
A
1625
B
25
C
35
D
925
Video Solution
Text Solution
The correct Answer is:B
Key Idea: According to conservation of energy, potential energy of height h=kinetic energy at ground.
Potential energy=Kinetic energy
ie,mgh=12mv2
⇒v=√2gh
If h1andh2 are intial and final heights, then
v1=√2gh1,v2=√2gh2
Loss in velocity
Δv=v1−v2=√2gh1−√2gh2
∴ fractional loss in velocity =Δvv1
=√2gh1−√2gh2√2gh1
=1−√h2h1
Substituting the values, we have
∴Δvv1=1−√1.85
=1−√0.36=1−0.6
=0.4=25
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.Bits velocity decreases and acceleration increases.Cits velocity increases and acceleration remains constant.Dits velocity and acceleration remains constant.A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
Ae2hBe√hCehD√ehA ball is dropped from a height of 100 m. At the surface of the earth, 20% of its energy is lost. To what height the ball will rise?
A80mB20mC40mD60m
A ball is dropped from height 10 m . Ball is embedded in sand 1 m and stops, then
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
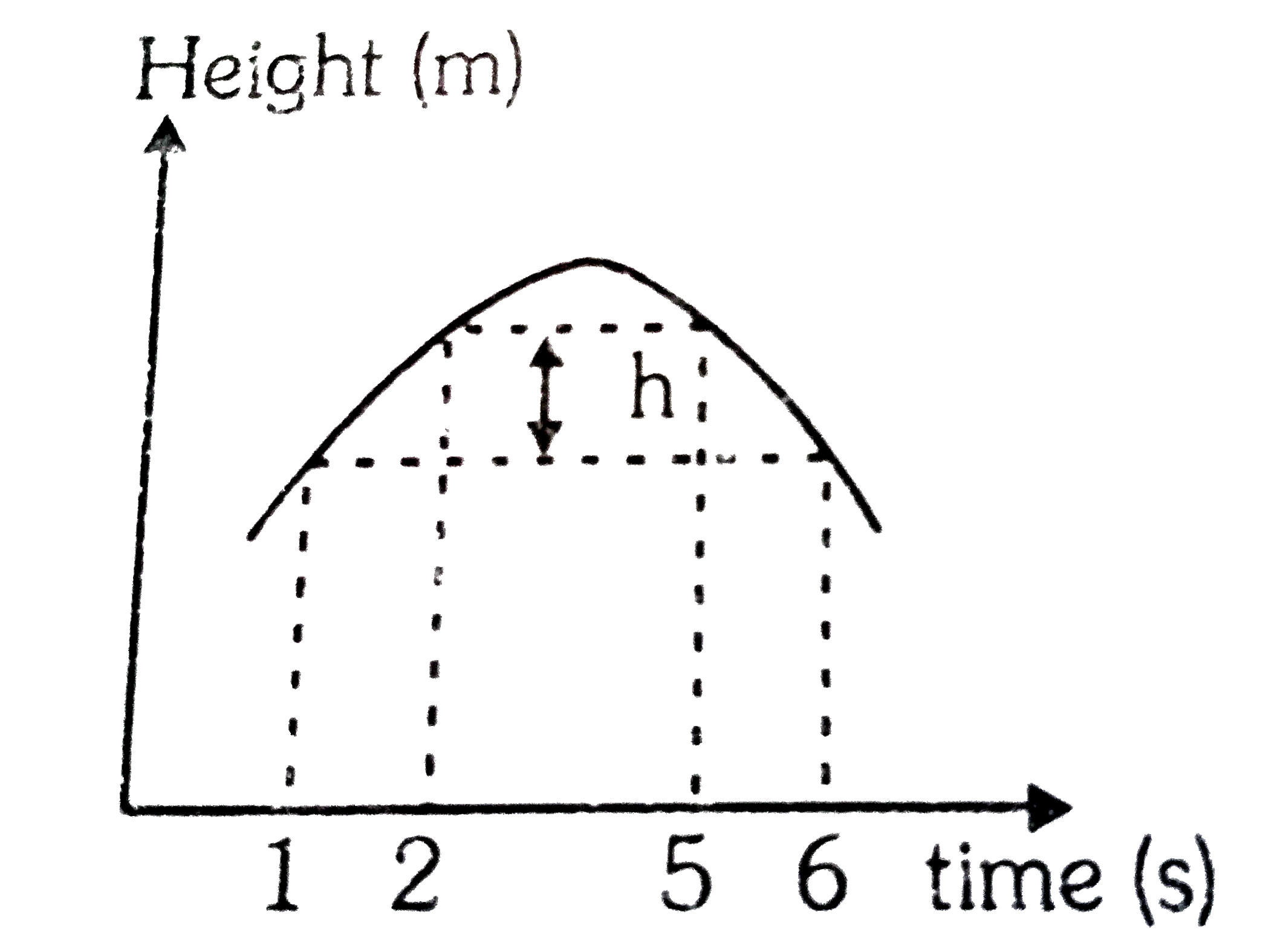
View SolutionA ball is dropped onto a floor from a height of 10m. If 20% of its initial energy is lost,then the height of bounce is
View SolutionA ball is dropped from a height of 5 m, if it rebound upto height of 1.8 m, then the ratio of velocities of the ball after and before rebound is :
View SolutionA rubber ball dropped from 24 m height loses its kinetic energy by 25%. What is the height to which it rebounds?
View Solution
