Given f(x)=ax+bx+1,limx→∞f(x)=1andlimx→0f(x)=2, then f(-2) is
0
1
2
3
The correct Answer is:A
Given limx→∞f(x)=1
limx→∞ax+bx+1=1
⇒limx→∞a+bx1+1x=1
⇒a=1
Also , limx→∞f(x)=2
⇒limx→∞ax+bx+1=2
⇒b=2
Now , f(-2)=a(−2)+b(−2)+1=−2+2−2+1=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let f(x)<0∀x∈(−∞,0)andf(x)>0∀x∈(0,∞) also f(0)=0, Again f'(x)<0∀x∈(−∞,−1)andf'(x)>∀x∈(−1,∞) also f'(−1)=0 given limx→∞f(x)=0andlimx→∞f(x)=∞ and function is twice differentiable.
The minimum number of points where f'(x) is zero is:A1B2C3D4Let f(x)<0∀x∈(≡∞,0)andf(x)>0∀x∈(0,∞) also f(0)=o, Again f'(x)<0∀x∈(−∞,−1)andf'(x)>∀x∈(−1,∞) also f'(−1)=0 given limx→∞f(x)=0andlimx→∞f(x)=∞ and function is twice differentiable.
If f'(x)<0∀x∈(0,∞)andf'(0)=1 then number of solutions of equatin f(x)=x2 is :A1B2C3D4
A function f(x) having the following properties,
(i) f(x) is continuous except at x=3
(ii) f(x) is differentiable except at x=-2 and x=3
(iii) f(0)=0limx→3f(x)→−∞limx→∞f(x)=3,limx→∞f(x)=0
(iv) f'(x)>0∀∈(−∞,−2)∪(3,∞) and f'(x)≤0∀x∈(−2,3)
(v) f''(x)>0∀x∈(−∞,−2)∪(−2,0) and f''(x)<0∀x∈(0,3)∪(3,∞)
Then answer the following questions
Find the Maximum possible number of solutions of f(x)=|x|
View SolutionLetf:R→R be a real function. The function f is double differentiable. If there exists n∈N and p∈R such that limx→∞xnf(x)=p and there exists limx→∞xn+1f(x),then
limx→∞xn+1f'(x) is equal to
View SolutionThe graph of y = f(x) is as shown in the following figure.
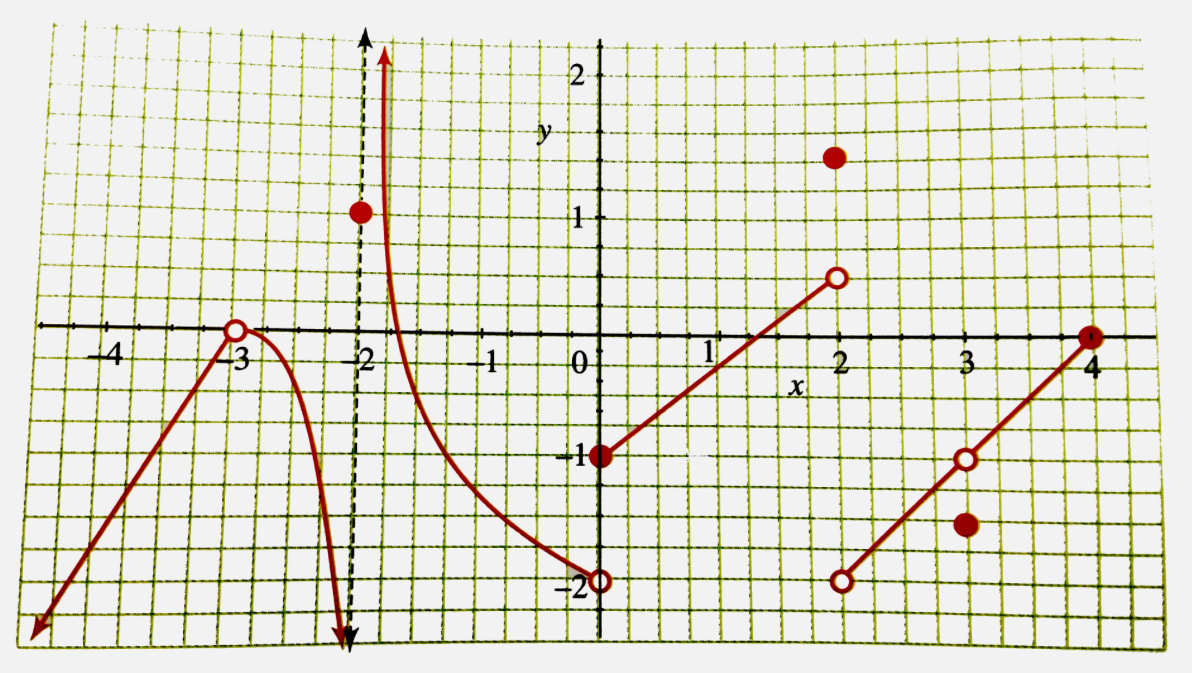
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionFor the function f(x)=2. Find limx→1f(x)
View SolutionLetf:R→R be a real function. The function f is double differentiable. If there exists n∈N and p∈R such that limx→∞xnf(x)=p and there exists limx→∞xn+1f(x),then
limx→∞xn+2f''(x) is equal to
View Solutionf(x)=ex then limx→0f(f(x))1f(x) is
View Solution
