Using the sine rule , prove the cosine rule.
By sine Rule, we have
asinA=bsinB=csinC=k(say)
∴a=k.sinA,b=k.sinB,c=k.sinC
Now consider b2+c2−a22bc
=k2.sin2B+k2.sin2C−k2sin2A2.ksinB.k.sinC
=k2(sin2B+sin2C−sin2A)2.ksinB.sinC
=sin2B+sin2C−sin2A2.sinB.sinC
=2sin2B+2sin2C−2sin2A4sinB.sinC
[Multiplying numerator and denominator by 2.]
=2sin2B+(1−cos2c)−(1−cos2A)4.sinB.sinC
=2sin2B+(cos2A−cos2C)4.sinB.sinC
=2sin2B+2sin(A+C).sin(C−A)4.sinB.sinC
=2sin2B+2sinB.sin(C−A)4sinB.sinC
⎡⎢⎣∵A+C=π−B∴sin(A+C)=sin(π−B)=sinB⎤⎥⎦
=2sinB(sinB+sin(C−A))4sinB.sinC
=sinB+sin(C−A)2sinC
=sin(C+A)+sin(C−A)2sinC
[∵sinB=sin(A+C)]
=2sinC.cosA2sinC=cosA
Hence, b2+c2−a22bc=cosA
Similarly, we can prove cosB=c2+a2−b22ca
cosC=a2+b2−c22ab
Hence, the cosine rule is proved.
Topper's Solved these Questions
- JULY 2018BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2018EXERCISE - SECTION II
20 Videos
- JULY 2017BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2017EXERCISE - SECTION - II
20 Videos
- MARCH 2014BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2014EXERCISE - SECTION-II
20 Videos
Similar Questions
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionSine formula proof :Sine Rule
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionIf A,BandC are the vetices of a triangle ABC, then prove sine rule asinA=bsinB=csinC.
View SolutionTheory OF Sine Rule || Cosine Rule || Projection formula
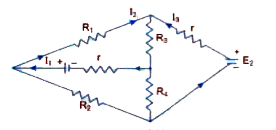
View SolutionState the two rules that serve as general rules for analysis of electrical circuits. Use these rules to write the three equations that may be used to obtain the values of the three unknown currents in the branches (shown) of the circuit
View SolutionFleming's left-hand rule is called as the motor rule and Fleming's right-hand rule is known as the generator rule.
View SolutionIllustrations Based upon Sine || Cosine Rule and Projection Formula
View SolutionBasic||Sine rule|| Cosine rule||Projection formula||Tangent rule || Napier Analogy
View Solution
