If $A (¯ a) and B (¯ b)$ are any two points in the space
and $R (¯ r)$ be a point on the line segment AB
dividing it internally in the ratio m : n , then prove that :
$¯ r = \frac{m ¯ b + n ¯ a}{m + n}$

Video Solution

Text Solution

Verified by Experts

As R is point on line segment AB (A - R - B ) and
$\frac{A R}{R B} = \frac{m}{n}$

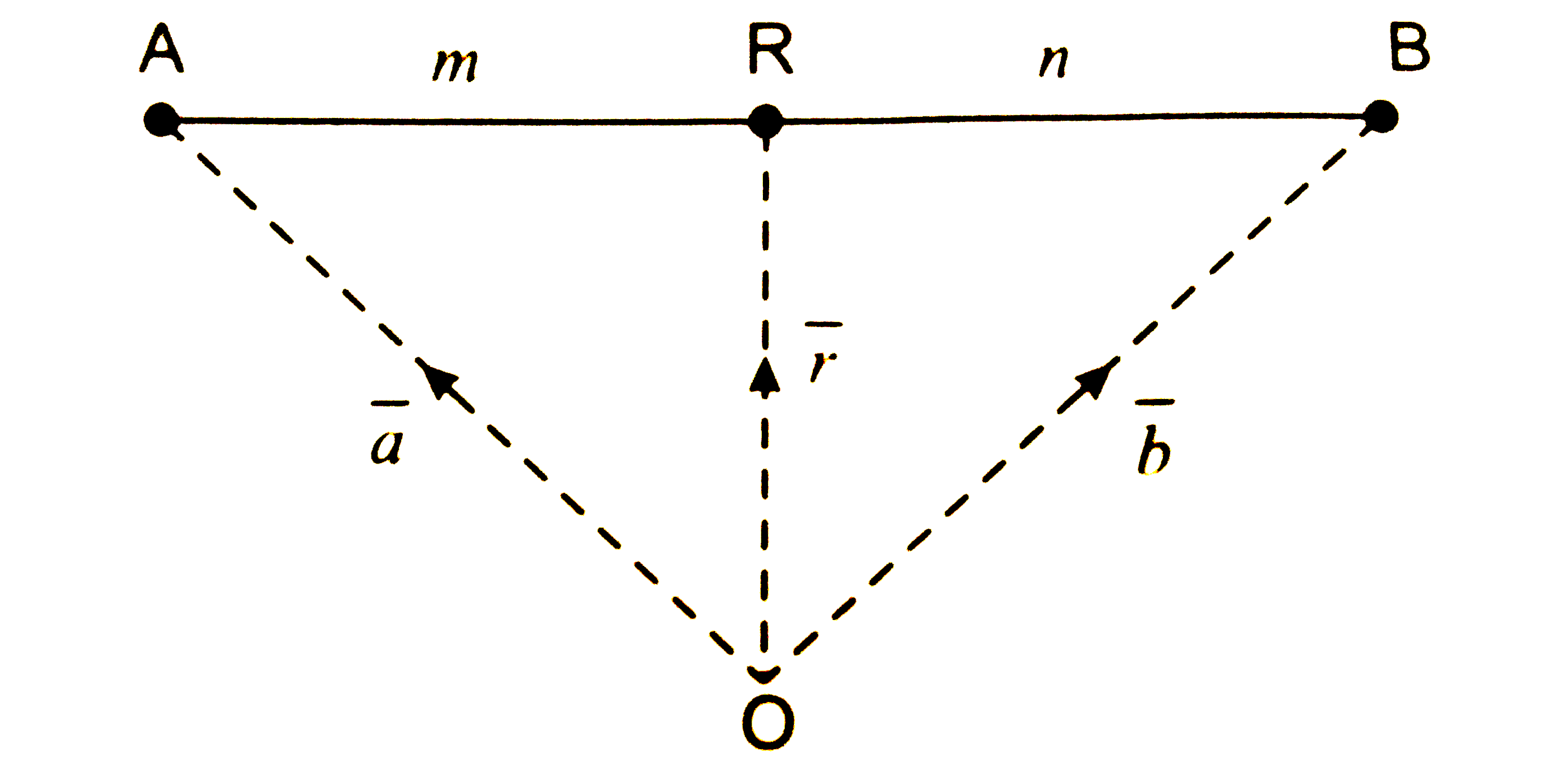
$∴ m (R B) = n (A R) and ¯ ¯¯¯¯ ¯ A R and ¯ ¯¯¯¯ ¯ A B$ are in same direction .
$∴ m ((¯ ¯¯¯¯ ¯ R B) = n (¯ ¯¯¯¯ ¯ A R)$
$\Rightarrow m (¯ ¯¯¯¯ ¯ O B - ¯ ¯¯¯¯ ¯ O R) = n (¯ ¯¯¯¯ ¯ O R - ¯ ¯¯¯¯ ¯ O A)$
$\Rightarrow m (¯ b - ¯ r) = n (¯ r - ¯ a)$
$\Rightarrow m ¯ b - m ¯ r = n ¯ r - n ¯ a$
$\Rightarrow m ¯ b + n ¯ a = m ¯ r + n^{2}$
$\Rightarrow ¯ r = \frac{m ¯ b + n ¯ a}{m + n}$ Hence Proved

Updated on:21/07/2023