Question

Determine a point which divides a line segment 7 cm long, internally in the ratio 2:3

Explanation

1. Draw a line segment AB=7cm by using a ruler.
2. Draw any ray making an acute `angleBAC` with AB.
3. Along AC, mark off (2+3)=5 point `A_(1),A_(2),A_(3),A_(4) " and " A_(5)` such that
`A A_(1)=A_(1)A_(2)=A_(2)A_(3)=A_(3)A_(4)=A_(4)A_(5)`.

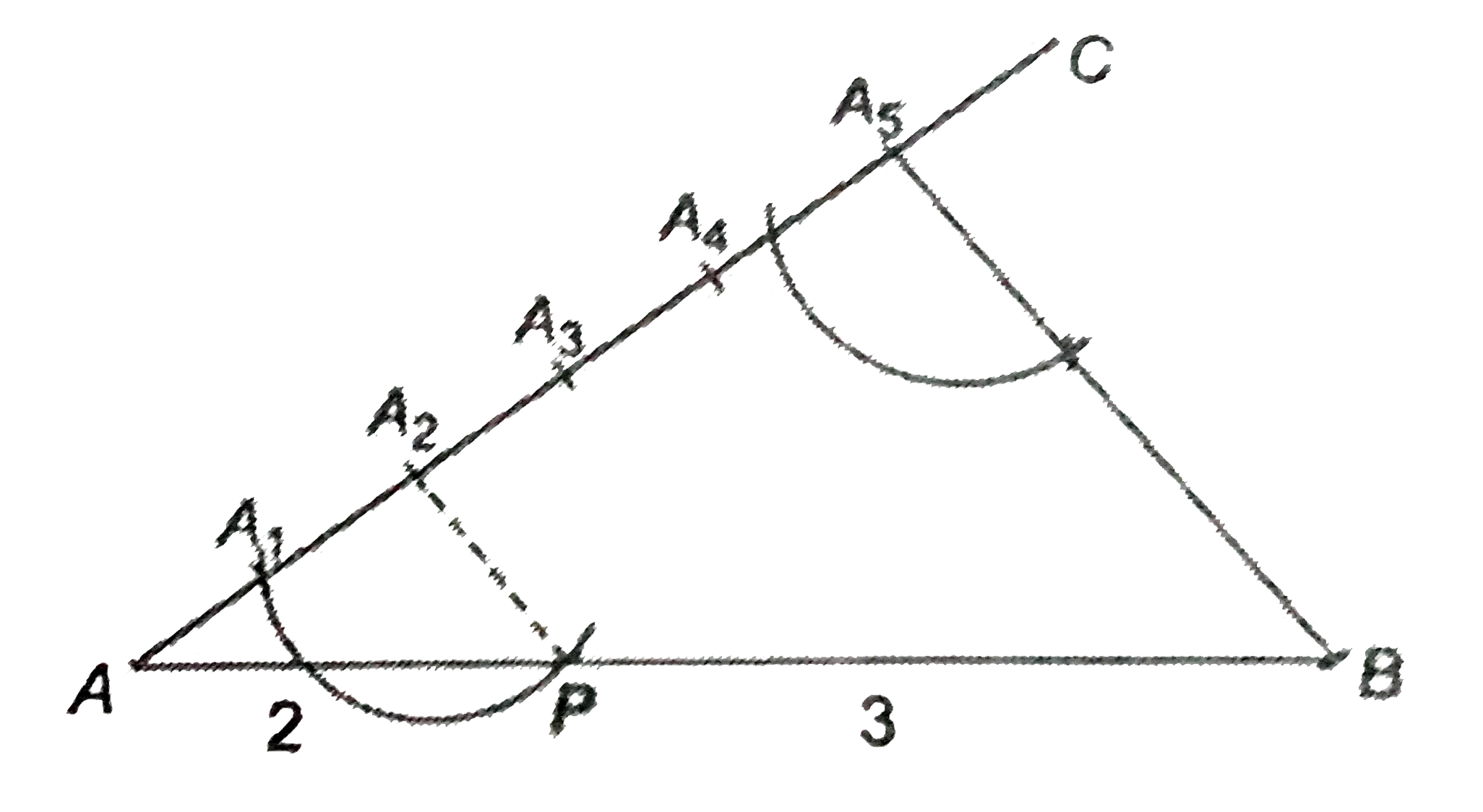
4. Join `BA_(5)`
5. Through `A_(2)` draw a line `A_(2)P` parallel to `A_(5)B` by making an angle equal to `angleAA_(5)B` at `A_(2)` intersecting AB at a point P.
The point P so obtained is the required point.
Justification: In `DeltaA A_(5)B`,
`A_(2)P||A_(5)B` ( construction )
`:. (A A_(2))/(A_(2)A_(5))=(AP)/(PB)` (by. B.P. theorem)
`implies (2)/(3)=(AP)/(PB)`(construction )
`implies AP:PB=2:3`
i.e., P divides AB internally in the ratio 2:3.
Alternate Method:
We can use one more method for this question.
1. Draw the line segment AB=7 cm
2.Draw any ray AC making an acute angle `angleBAC` with AB.
3. Draw a ray BD parallel to AC by making ` angle ABC` equal to angle `angleBAC`.
4. Mark off 2 points `A_(1)` and `A_(2)` on AC and 3 points `B_(1), B_(2), B_(3)` on AD such that
`A A_(1)=A_(1)A_(2)=BB_(1)=B_(1)B_(2)=B_(2)B_(3)`
5. Join `B_(3)A_(2)`, suppose it intersect AB at point P. Then, P is the require point.