Wavelengths of two notes in air are $(\frac{90}{175})$ m and $(\frac{90}{173})$ m. Each note produces four beats per second with a third note of a fixed frequency. Calculate the velocity of sound in air.

Video Solution

Text Solution

Verified by Experts

The lowest allowed frequency of vibration (fundamental ) of a bounded medium and all its integral multiples are called harmonics.
The stationary wave in the air column are subject to two boundary condition that there must be a node at the closed end and an antinode at the open end. In the following we shall ignore the end correction.

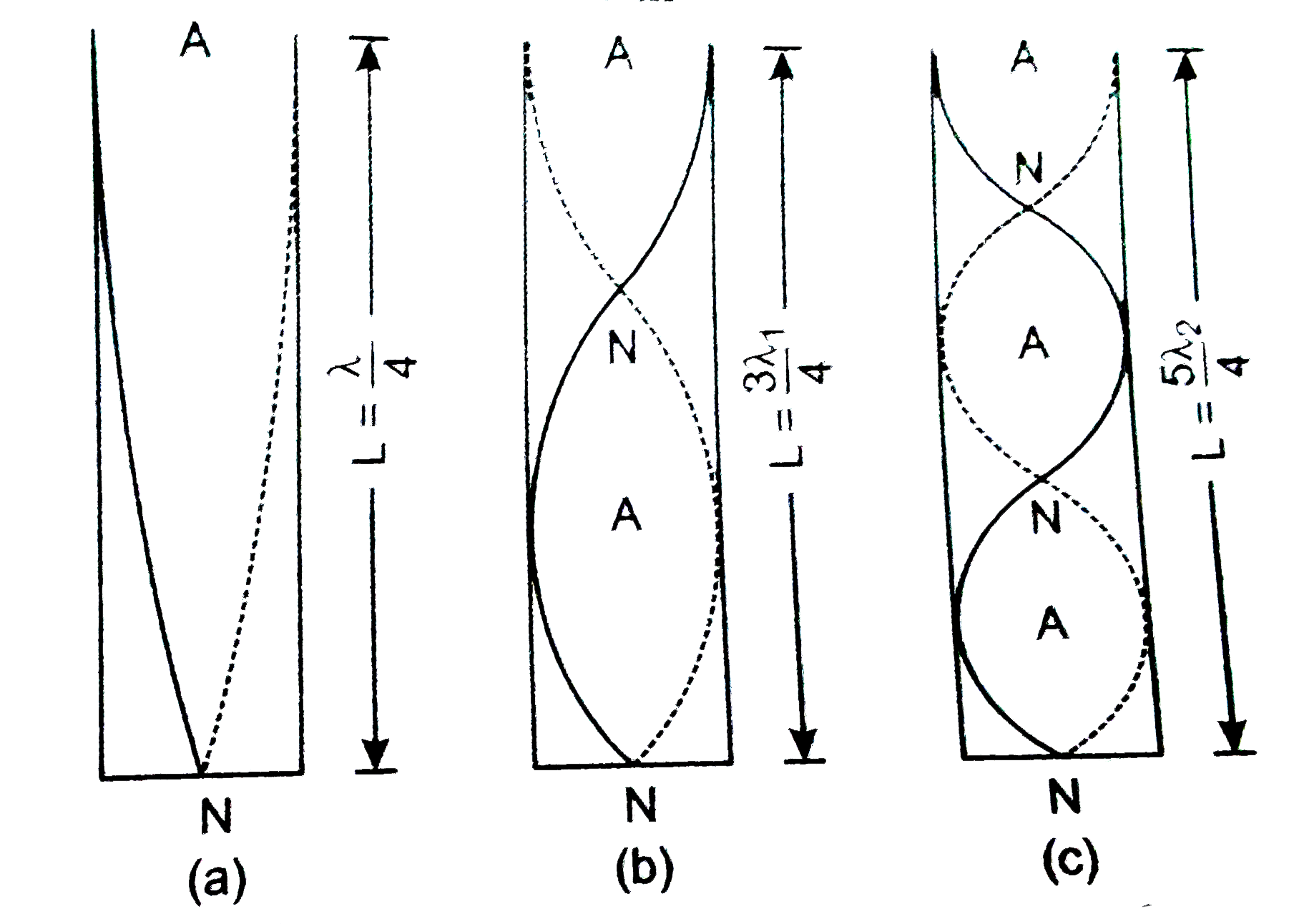
Let, v be speed of sound of sound in air, In the simplest mode of vibration as shown in the figure.
(a) There is a one node at the closed end and an antinode at the open end. The distance between a node and a constructive antinode is $λ / 4$ , where $λ$ is the wavelength of sound. The corresponding wavelength $λ$ and frequency $η$ are
$λ = 4 L and n = \frac{v}{λ} = \frac{v}{4 L}$ ...(i)
This gives the fundamental frequency of vibration, the first overtone, two nodes and two antinodes are formed as shown in the figure (b). The corresponding wavelength $λ_{1}$ and frequency $n_{1}$ are
$λ_{1} = \frac{4 L}{3} and n_{1} = \frac{v}{λ_{1}} = \frac{3 v}{4 L} = 3 n$ ...(ii)
Therefore, the frequency in the first overtone is three times the fundamental frequency i.e., the first overtone is the third harmonic.
(c ) In the second ovetone, three nodes and three antinodes are formed as shown in the figure (c ).
The corresponding wavelength $λ_{2}$ and frequency $n_{2}$ are
$λ_{2} = \frac{4 L}{5} and n_{2} = \frac{v}{λ_{2}} = \frac{5 v}{4 L} = 5 n$ ....(iii)
which is the fifth harmonic.
Therefore, in general the frequency of the $p^{t h}$ overtone (p = 1, 2, 3, ......) is
$n_{p} = (2 p + 1) n$ ...(iv)
i.e., the $p^{t h}$ overtone is the ${(2 p + 1)}^{t h}$
harmonic.
Equation (i), (ii) and (iii) show that allowed frequencies in an air column is a pipe closed at one end are $n, 3 n, 5 n ... ... . .$
That is only odd harmonics are present as overtones.
Nomerical :
Given : $λ_{1} = \frac{81}{173} m, λ_{2} = \frac{81}{170} m .$
Let, $n_{1} and n_{2}$ be the corresponding frequencies.
$∴ v = n_{1} λ_{1} = n_{2} λ_{2}$
where, v is the speed of sound in air.
$∴ n_{1} = \frac{v}{λ_{1}} and n_{2} = \frac{v}{λ_{2}}$ ...(i)
But $λ_{2} > λ_{1}$
$∴ n_{2} < n_{1}$
$∴ n_{1} - n_{2} = 10$
$\frac{v}{λ_{1}} - \frac{v}{λ_{2}} = 10$
$v [\frac{1}{λ_{1}} - \frac{1}{λ_{2}} = 10$
$v [\frac{173}{81} - \frac{170}{81}] = 10$
$v [\frac{3}{81}] = 10$
$v = \frac{10 \times 81}{3} = 270 m / s .$

Updated on:21/07/2023

The wavelength of two sound notes in air are $\frac{40}{195} m$ and $\frac{40}{193} m$ . Each note produces $9$ beats per second, separately with a third note of fixed frequency. The velocity of sound in air in m//s is
A360
B320
C300
D340
Wavelength of two notes in air are 1 m and $1 \frac{1}{164}$ m. Each note produces 1 beats/s with a third note of a fixed frequency. The speed of sound in air is
A $330 m / s$
B $340 m / s$
C $350 m / s$
D $328 m / s$
Wavelengths of two sound notes in air are $\frac{80}{177}$ m and $\frac{80}{175} m$ respectively. Each note of a fixed frequency. What is the velocity of sound in air?
A300 m/s
B320 m/s
C310 m/s
D350 m/s