The difference in tensions in the string at lowest and highest points in the path of the particle of mass 'm' performing vertical circular motion is :
2mg
4 mg
6mg
8 mg
The correct Answer is:C
To find the difference in tensions in the string at the lowest and highest points of a particle of mass 'm' performing vertical circular motion, we can follow these steps:
Step 1: Analyze Forces at the Lowest Point
At the lowest point of the circular motion, the forces acting on the mass 'm' are:
- The tension in the string (T_low)
- The weight of the mass (mg)
At this point, the net force provides the centripetal force required for circular motion. Therefore, we can write the following equation:
Tlow−mg=mv2r
Where:
- Tlow = tension at the lowest point
- mg = weight of the mass
- v = speed of the mass at the lowest point
- r = radius of the circular path
Rearranging gives us:
Tlow=mg+mv2r
Step 2: Analyze Forces at the Highest Point
At the highest point of the circular motion, the forces acting on the mass 'm' are:
- The tension in the string (T_high)
- The weight of the mass (mg)
At this point, the equation for the net force is:
Thigh+mg=mv2r
Rearranging gives us:
Thigh=mv2r−mg
Step 3: Calculate the Difference in Tension
Now, we need to find the difference in tension between the lowest and highest points:
ΔT=Tlow−Thigh
Substituting the expressions we derived:
ΔT=(mg+mv2r)−(mv2r−mg)
Simplifying this expression:
ΔT=mg+mv2r−mv2r+mg
ΔT=2mg
Final Result
Thus, the difference in tensions in the string at the lowest and highest points in the path of the particle is:
ΔT=2mg
---
At the lowest point of the circular motion, the forces acting on the mass 'm' are:
- The tension in the string (T_low)
- The weight of the mass (mg)
- Tlow = tension at the lowest point
- mg = weight of the mass
- v = speed of the mass at the lowest point
- r = radius of the circular path
At the highest point of the circular motion, the forces acting on the mass 'm' are:
- The tension in the string (T_high)
- The weight of the mass (mg)
Now, we need to find the difference in tension between the lowest and highest points:
Thus, the difference in tensions in the string at the lowest and highest points in the path of the particle is:
Topper's Solved these Questions
- BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2016EXERCISE - SECTION -II21videos
JULY 2016
- BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - FEBRUARY 2019EXERCISE - SECTION-D6videos
FEBRUARY 2019
- BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2017EXERCISE - SECTION-I12videos
JULY 2017
Similar Questions
Derive an expression for the difference in tensions at the highest and lowest points for a particle performing vertical circular motion.
View SolutionA stone of mass 0.3 kg is tied to one end of a string 0.8 m long and rotated in a vertical circle. At what speed of the ball will the tension in the string be zero at the highest point of the circle? What would be the tension at the lowest point in this case ? Given g=9.8ms−2 ?
View Solution
Knowledge Check
- Question 1 - Select One
A particle (bob) of mass 1 kg is performing vertical cicular motion. Then :
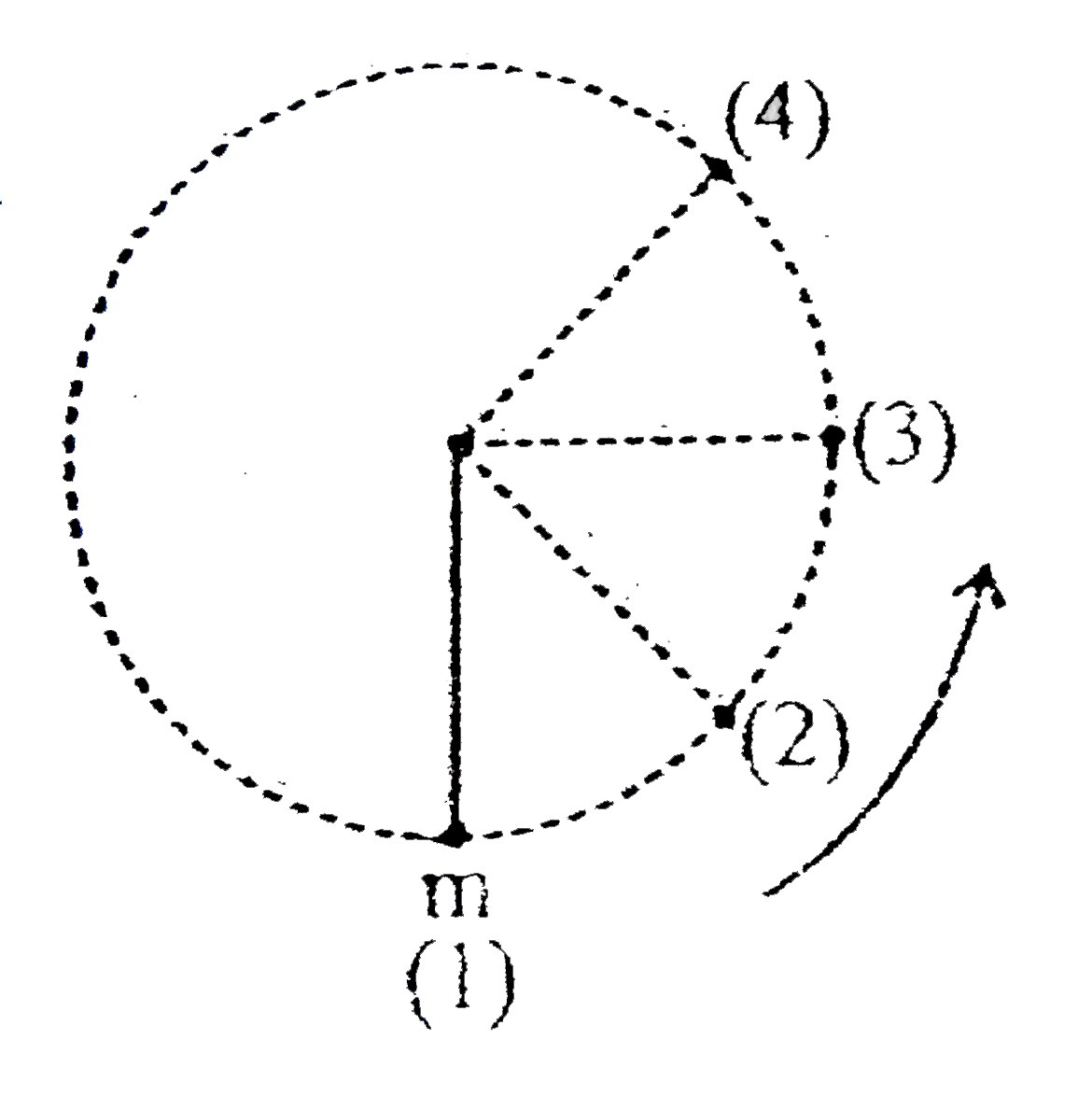 APower delevered by tension at point (4) is negative.BPower delevered by tension at point (2) is positive.CPower delivered by gravitational force at point (3) is zero.DPower delivered by gravitational force at point (4) is negative.
APower delevered by tension at point (4) is negative.BPower delevered by tension at point (2) is positive.CPower delivered by gravitational force at point (3) is zero.DPower delivered by gravitational force at point (4) is negative. - Question 2 - Select One
A particle performing uniform circular motion has
Aradial velocity and radial accelerationBradial velocity and transverse accelerationCtransverse velocity and radial accelerationDtransverse velocity and transverse acceleration - Question 3 - Select One
A particle performing uniform circular motion has
ARadial velocity and radial accelerationBA radial velocity and transverse accelerationCTransverse velocity and radial accelerationDTransverse velocity and transverse acceleration
For a particle performing a uniform circular motion the acceleration is
View SolutionA particle is performing uniforme circular motion, has constant
View SolutionThe maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
View SolutionA small stone of mass 0.4 kg tied to a massless inextensible string is made to loop the loop Radius of the path is 4 m. Find its speed at the highest point. How would this speed change if mass of the stone is decoreased by 10%?(g=10ms−2).
View SolutionA point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
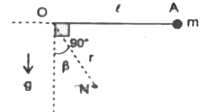 View Solution
View Solution

