Derive an expression for the difference in tensions at the highest and lowest points for a particle performing vertical circular motion.

Text Solution

Verified by Experts

Consider a small body ( or particle) of mass m tied to a string and revolved in a vertical circle of radius r at a place where the accerleration due to graviy is g. At every instant of its motion, the body is acted upon by two forces, namely, its weight $- \to m g$ and the tension $\to T$ in the string.

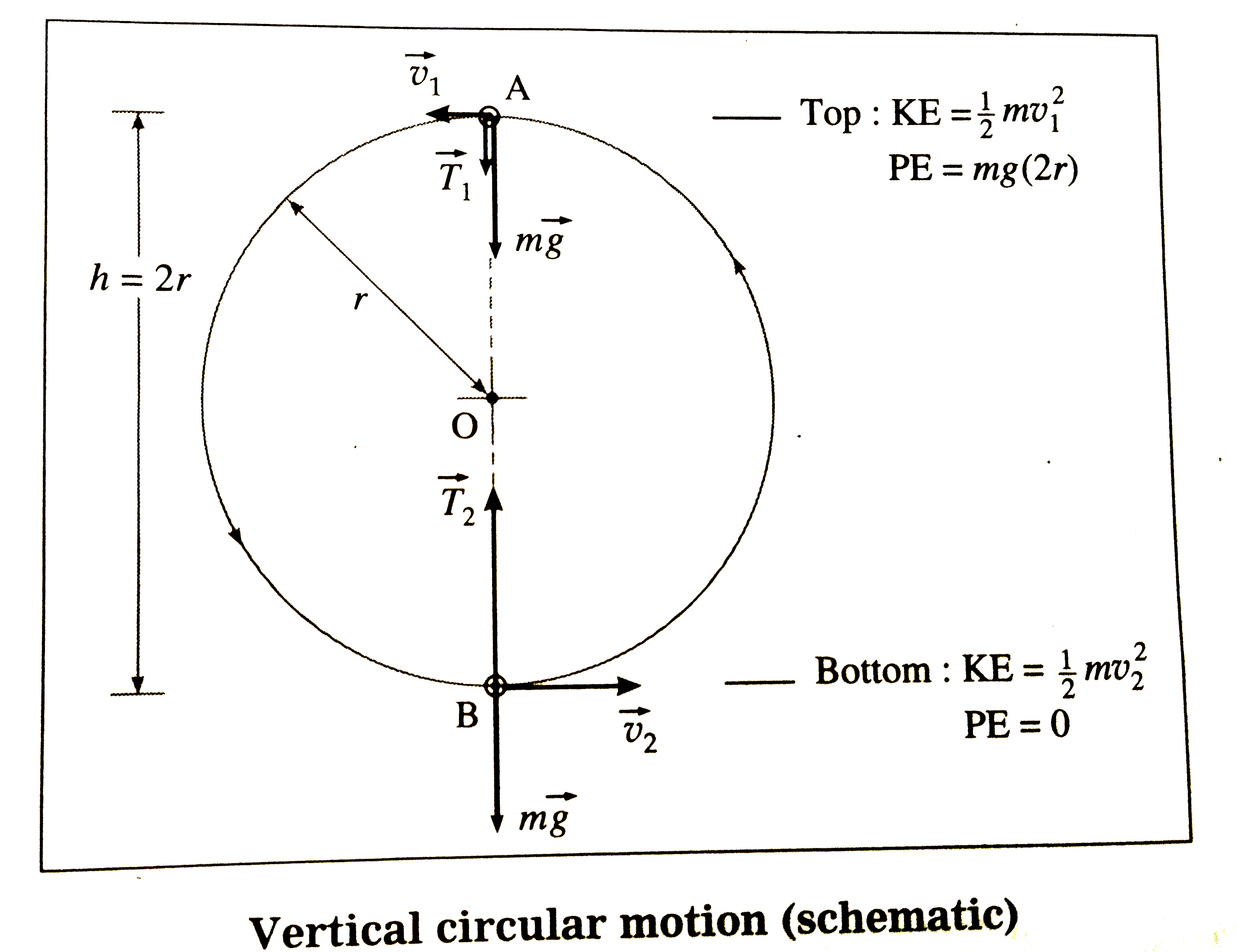
let $v_{2}$ be the speed of body and $T_{2}$ be the tension in the string at the lowest point B . We take the reference level for zero potential energy to be the bottom of the circle. THen, the body has only kinetic energy $\frac{1}{2} m v_{2}^{2}$ at the lowest point.
$∴ T_{2} = \frac{m v_{2}^{2}}{r} + m g ... (1)$
and the total energy at the bottom $= K E + P E = \frac{1}{2} m v_{2}^{2} + 0$
$= \frac{1}{2} m v_{2}^{2} ... (2)$
Let $v_{1}$ be the speed and $T_{1}$ the tension in the string at the highest point A. As the body goes from B to A, it rises through a height h = 2r.
$∴ T_{1} = \frac{m v_{1}^{2}}{r} - m g ... (3)$
and the total energy at A = KE + PE
$= \frac{1}{2} m v_{1}^{2} + m g (2 r) ... (4)$
Thus, from Eqs. (1) and (3),
$T_{2} - T_{1} = \frac{m v_{2}^{2}}{r} + m g - (\frac{m v_{1}^{2}}{r} - m g)$
$= \frac{m}{r} (v_{2}^{2} - v_{1}^{2}) + 2 m g ... (5)$
Assuming that the total energy of the body is conserved, the totl energy at the bottom = total energy at the top
Then, from Eqs. (2) and (4),
$\frac{1}{2} m v_{2}^{2} = \frac{1}{2} m v_{1}^{2} + m g (2 r)$
$∴ v_{2}^{2} - v_{1}^{2} = 4 g r ... (6)$
Substituting this in Eq. (5),
$T_{2} - T_{1} = \frac{m}{r} (4 g r) + 2 m g$
$= 4 m g + 2 m g$
= 6 mg
Therefore, the difference in the tensions in the string at the highest and the lowest points in 6 times the weight of the body.

Updated on:21/07/2023

A particle performing uniform circular motion has
Aradial velocity and radial acceleration
Bradial velocity and transverse acceleration
Ctransverse velocity and radial acceleration
Dtransverse velocity and transverse acceleration
A particle performing uniform circular motion has
ARadial velocity and radial acceleration
BA radial velocity and transverse acceleration
CTransverse velocity and radial acceleration
DTransverse velocity and transverse acceleration
A particle is performing uniforme circular motion, has constant
Avelocity
Bkinetic energy
Cmomentum
Dacceleration