In the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
We can join OB and OC.
Now, in ΔOABandΔODC
OA=OD (Both are radius)
OB=OC (Both are radius)
∠AOB=∠DOC (vertically opposite angles)
∴ΔOAB≅ΔODC (By SAS congruency)
∴AB=DC
Similar Questions
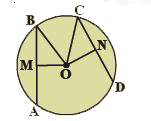
In the figure, O is the centre of the circle and AB = CD. OM is perpendicular on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯ON is perpendicular on ¯¯¯¯¯¯CD. Then prove that OM = ON.

View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on bar(AB) and bar(ON) is perpendicular on bar(CD) . Then prove that OM = ON.
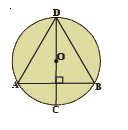
View SolutionIn the adjacent figure, AB is a chord of circle with centre O. CD is the diameter perpendicualr to AB. Show that AD = BD
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯ON is perpendicular on ¯¯¯¯¯¯CD. Then prove that OM = ON.
View SolutionIn the adjacent figure, AB is a chord of circle with centre O. CD is the diameter perpendicualr to AB. Show that AD = BD
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯ON is perpendicular on ¯¯¯¯¯¯CD. Then prove that OM = ON.
View SolutionIn the adjacent figure, AB is a chord of circle with centre O. CD is the diameter perpendicualr to AB. Show that AD = BD
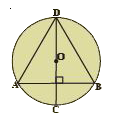
View SolutionAB and CD are the diameters of a circle. Prove that ABCD is a rectangle.
View Solution
