In Figure, O is the center of a circle and PO bisects ∠APD Prove that AB=CD
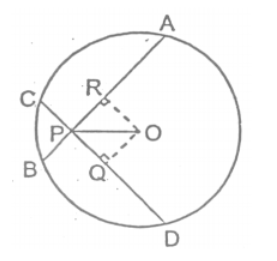
Step by step video & image solution for In Figure, O is the center of a circle and P O bisects /_APD Prove that AB=CD by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, O is the centre of a circle and arc ABC subtends an angle of 130∘ at O. AB is extended to P, Then, ∠PBC is equal to
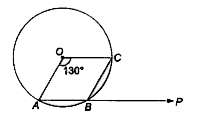 A25∘B40∘C65∘D75∘
A25∘B40∘C65∘D75∘
In Figure, AB=CB and O is the centre of the circle. Prove that BO bisects ∠ABC.
View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View SolutionIn the figure, O is the center of the circle and BO is the bisector of angle ABC show that AB=BC
View SolutionIn Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
View SolutionIn the given figure, a straight line l passing through the centre O of the circle bisects the chord AB and CD. Prove that AB||CD.
View SolutionIf figure, O is the centre of the circle, BD=ODandCD⊥AB. Find∠CAB.

View Solution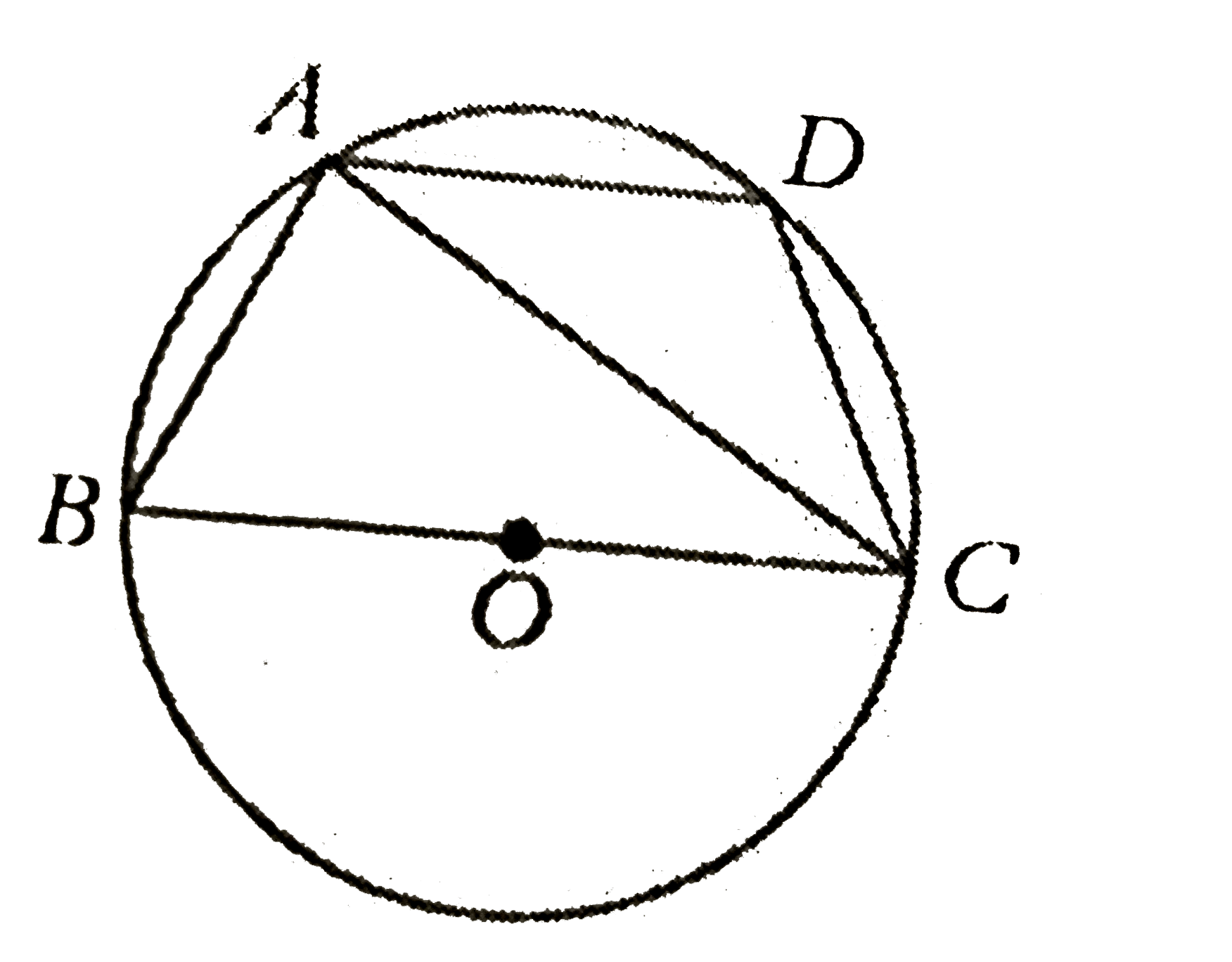
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
View Solution
