Find the mean deviation about the mean for the data : 4,7,8,9,10,12,13,17
To find the mean deviation about the mean for the data set 4,7,8,9,10,12,13,17, we will follow these steps:
Step 1: Calculate the Mean
The mean is calculated using the formula:
Mean=Sum of all dataNumber of data points
First, we find the sum of the data:
4+7+8+9+10+12+13+17=90
Now, we divide by the number of data points (which is 8):
Mean=908=11.25
Step 2: Calculate the Deviations from the Mean
Next, we find the deviations of each data point from the mean:
- For 4: 4−11.25=−7.25
- For 7: 7−11.25=−4.25
- For 8: 8−11.25=−3.25
- For 9: 9−11.25=−2.25
- For 10: 10−11.25=−1.25
- For 12: 12−11.25=0.75
- For 13: 13−11.25=1.75
- For 17: 17−11.25=5.75
Step 3: Take the Absolute Values of Deviations
Now, we take the absolute values of these deviations:
- |−7.25|=7.25
- |−4.25|=4.25
- |−3.25|=3.25
- |−2.25|=2.25
- |−1.25|=1.25
- |0.75|=0.75
- |1.75|=1.75
- |5.75|=5.75
Step 4: Calculate the Sum of Absolute Deviations
Now we sum these absolute deviations:
7.25+4.25+3.25+2.25+1.25+0.75+1.75+5.75=26.5
Step 5: Calculate the Mean Deviation
Finally, we calculate the mean deviation using the formula:
Mean Deviation=Sum of Absolute DeviationsNumber of Data Points=26.58=3.3125
Thus, the mean deviation about the mean for the given data is 3.3125.
---
The mean is calculated using the formula:
Mean=Sum of all dataNumber of data points
First, we find the sum of the data:
4+7+8+9+10+12+13+17=90
Now, we divide by the number of data points (which is 8):
Mean=908=11.25
Next, we find the deviations of each data point from the mean:
- For 4: 4−11.25=−7.25
- For 7: 7−11.25=−4.25
- For 8: 8−11.25=−3.25
- For 9: 9−11.25=−2.25
- For 10: 10−11.25=−1.25
- For 12: 12−11.25=0.75
- For 13: 13−11.25=1.75
- For 17: 17−11.25=5.75
Now, we take the absolute values of these deviations:
- |−7.25|=7.25
- |−4.25|=4.25
- |−3.25|=3.25
- |−2.25|=2.25
- |−1.25|=1.25
- |0.75|=0.75
- |1.75|=1.75
- |5.75|=5.75
Now we sum these absolute deviations:
7.25+4.25+3.25+2.25+1.25+0.75+1.75+5.75=26.5
Finally, we calculate the mean deviation using the formula:
Mean Deviation=Sum of Absolute DeviationsNumber of Data Points=26.58=3.3125
Topper's Solved these Questions
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.3
5 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.2
10 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - SOLVED EXAMPLES
18 Videos
- SETSBOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.5
7 Videos
- STRAIGHT LINESBOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.5
2 Videos
Similar Questions
Knowledge Check
What is the mean deviation about the mean for the data 4, 7, 8, 9, 10, 12, 13, 17?
A2.5B3C3.5D4What is the mean deviation about the mean for the data 4, 7, 8, 9, 10, 12, 13 and 17?
A2.5B3C3.25D4Find the mean deviation about the mean for the following data : 6, 7, 10, 12, 13, 4, 8, 12.
A3.76B2C2.75D2.55
Find the mean deviation about the mean for the data is Question:

View SolutionFind the mean deviation about the mean for the data in Question:

View SolutionFind the mean deviation about the mean for the data in Question:

View SolutionFind the mean deviation about the mean for the following data :
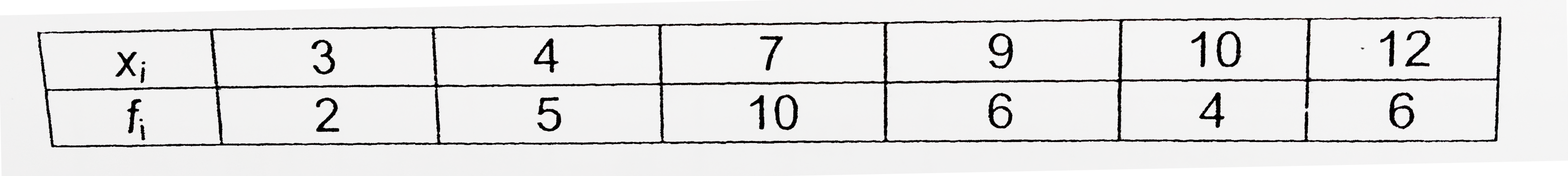
View SolutionFind the mean deviation about the mean for the following data :

View Solution

