Question

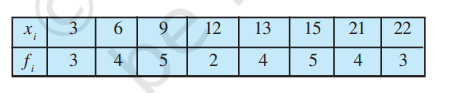
Find the mean deviation about the median for the data : $x_i$ 15 21 27 30 35 $f_i$ 3 5 6 7 8

Explanation

To find the mean deviation about the median for the given data, we will follow these steps:

Step 1: Organize the Data
We have the following data:
- \(x_i\): 15, 21, 27, 30, 35
- \(f_i\): 3, 5, 6, 7, 8

Step 2: Calculate the Total Frequency
First, we need to calculate the total frequency \( \Sigma f_i \):
\( \Sigma f_i = 3 + 5 + 6 + 7 + 8 = 29 \)

Step 3: Find the Cumulative Frequency
Next, we find the cumulative frequency to determine the median:
- For \(x_1 = 15\), cumulative frequency = 3
- For \(x_2 = 21\), cumulative frequency = 3 + 5 = 8
- For \(x_3 = 27\), cumulative frequency = 8 + 6 = 14
- For \(x_4 = 30\), cumulative frequency = 14 + 7 = 21
- For \(x_5 = 35\), cumulative frequency = 21 + 8 = 29

Step 4: Determine the Median
The median is found at the position \( \frac{n}{2} \) where \( n = \Sigma f_i = 29 \). Thus, we look for the 15th term:
- The 15th term falls in the cumulative frequency of 21 (which corresponds to \(x = 30\)).

So, the median \(M\) is:
\( M = 30 \)

Step 5: Calculate \( |x_i - M| \)
Now we calculate \( |x_i - M| \) for each \(x_i\):
- For \(x_1 = 15\): \( |15 - 30| = 15 \)
- For \(x_2 = 21\): \( |21 - 30| = 9 \)
- For \(x_3 = 27\): \( |27 - 30| = 3 \)
- For \(x_4 = 30\): \( |30 - 30| = 0 \)
- For \(x_5 = 35\): \( |35 - 30| = 5 \)

Step 6: Calculate \( f_i \cdot |x_i - M| \)
Next, we multiply each \( |x_i - M| \) by the corresponding frequency \(f_i\):
- For \(x_1\): \(3 \cdot 15 = 45\)
- For \(x_2\): \(5 \cdot 9 = 45\)
- For \(x_3\): \(6 \cdot 3 = 18\)
- For \(x_4\): \(7 \cdot 0 = 0\)
- For \(x_5\): \(8 \cdot 5 = 40\)

Step 7: Sum of \( f_i \cdot |x_i - M| \)
Now we sum these products:
\( \Sigma (f_i \cdot |x_i - M|) = 45 + 45 + 18 + 0 + 40 = 148 \)

Step 8: Calculate the Mean Deviation
Finally, we calculate the mean deviation using the formula:
\( \text{Mean Deviation} = \frac{\Sigma (f_i \cdot |x_i - M|)}{\Sigma f_i} = \frac{148}{29} \approx 5.10 \)

Final Answer
The mean deviation about the median is approximately \(5.10\).

---