आयत ABCD के अंदर स्थित बिंदु O को इसके शीर्षों से मिलाया जाता है । सिद्ध कीजिये कि इस प्रकार बने सम्मुख त्रिभुजों के एक युग्म के क्षेत्रफलों का योगफल, दूसरे सम्मुख त्रिभुजों के युग्म के क्षेत्रफलों के योगफल के बराबर होता है।
दिया है : एक आयत ABCD तथा इसके अंदर स्थित बिंदु O , जिसको शीर्षों A , B , C तथा D से मिलाया गया है।
सिद्ध करना है : ar(AOD)+ar(ΔBOC)=ar(ΔAOB)+ar(ΔCOD)
रचना : EOF ।। AB तथा LOM ।।AD खींचिये।
उपपत्ति : चूँकि
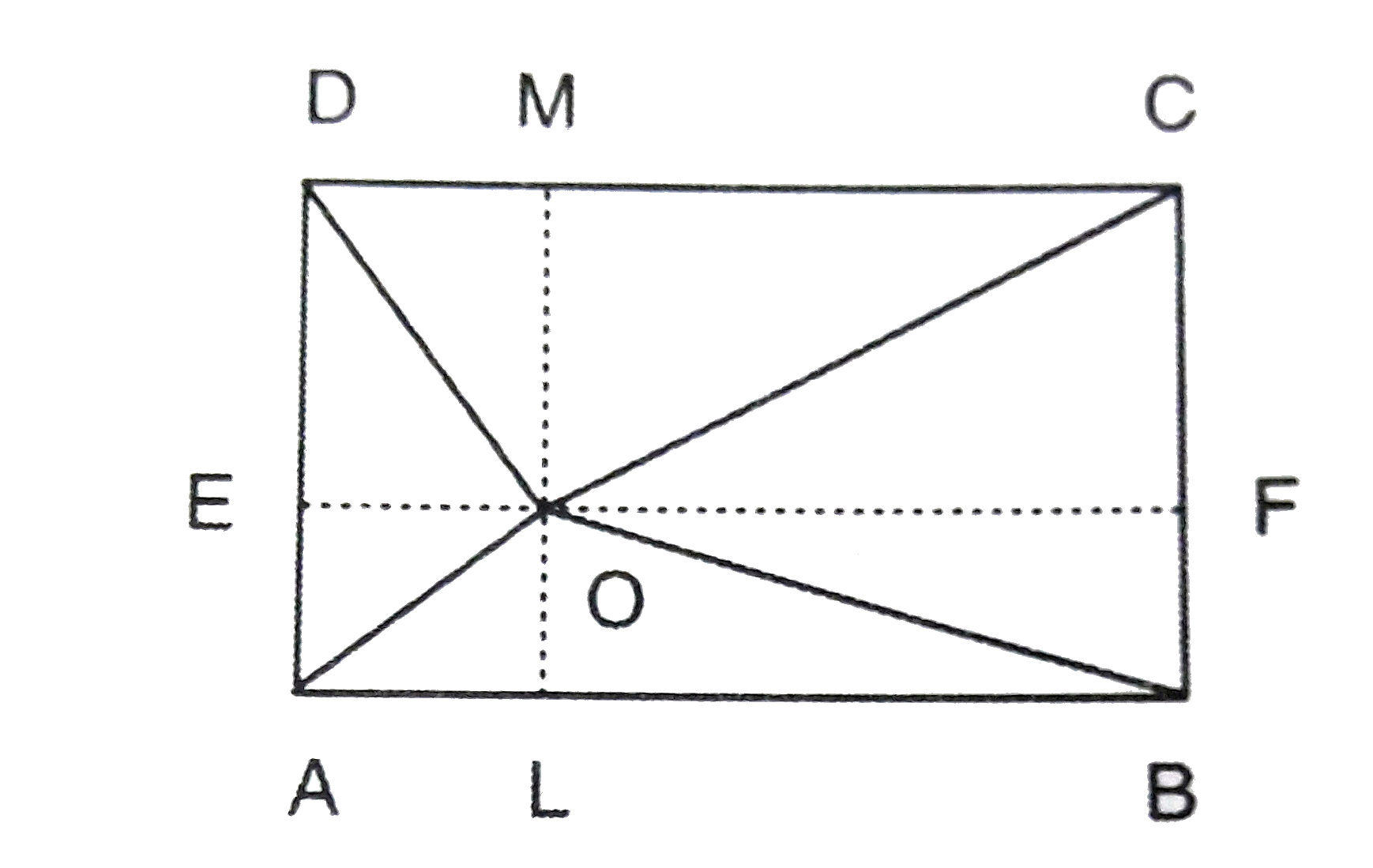
ar(ΔAOD)+ar(ΔBOC)=12(AD×BC)+12(BC×OF)
=12(AD×OE)+12(AD×OF) [∵AD=BC]
=12(AD×(OE+OF))
=12(AD×EF)
=12(AD×AB) [∵EF=AB]
=12ar(आयत ABCD )
तथा ar(ΔAOB)+ar(ΔCOD)=12(AB×OL)+12(CD×OM)
=12(AB×OL)+12(AB×OM) [∵AB=CD]
=12AB×(OL+OM)
=12(AB×LM)
=12(AB×AD) [∵LM=AD]
=12ar[आयत ABCD]
∴ar(ΔAOD)=ar(ΔBOC)=ar(ΔAOB)+ar(ΔCOD)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण
1 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.1
6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solutionदो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 5:3 है, तो उनके संगत भुजाओं का अनुपात है :
View Solutionसमरूप त्रिभुजों के क्षेत्रफल
View Solutionसदिशों का योगफल|सदिश योगफल के गुणधर्म#!#एक अदिश से सदिश का गुणन#!#एक सदिश के घटक#!#उदाहरण
View Solutionकोणों के प्रकार |कोणों का रेखिक युग्म |प्रतिच्छेदी तथा अप्रतिच्छेदी रेखाएं |कोणों के युग्म से संबंधित अभिक्रियाएँ |प्रमेय 6.1|सारांश
View Solutionत्रिभुज |त्रिभुजों के प्रकार |सर्वांगसम आकृतिया |त्रिभुजों का सर्वांगसमता |सारांश
View Solutionउस शब्द-युग्म का चयन करें, जिस में शब्दों के बीच वही संबंध है, जो संबंध दिए गए शब्द-युग्म के शब्दों के बीच है।
तीव्र : धीमा
View Solutionसमरूप त्रिभुजों के क्षेत्रफल
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution2 N HCI के 25 ml, 4 N HNO_3 के 50 ml और 2 M H_2SO_4 के v ml को एक साथ मिलाया जाता है और कुल आयतन को 1 L तक तैयार किया जाता है, तनुकरण के बाद इस अम्ल मिश्रण का 50 ml, 1 N Na_2CO_3 के 25 ml के साथ पूर्णतया अभिक्रिया करता है। v का मान है
View Solution
